2004年12月27日
電場・電位の概念(初心者用)
目次
目標
電場E・電位Vの意味を一様な重力場と比較して説明します。
初心者向けのかなり荒っぽい解説ですが、電場E、電位Vがさっぱり分からない人には理解のヒントになると思います。
場と場の力
ある空間にいるだけで物体に必ず働く力を場の力といいます。 そのような空間は場とよばれます。 たとえば、私たちのいる地球表面では重力(=質量m×重力加速度g)がすべての物体に必ず働きます。 だから重力は場の力といえます。そして重力の働く空間である地球は重力場と呼ばれています。場の力が生まれるのには原因があります。
地球表面の重力場の場合、地球が質量を持っていることによります。
電場と電場から受ける力
電気が帯びている周りには電場が発生します。
つまり、電気量q(物体がどれだけ電気を帯びているかを表す物理量)
を持っていることが電場の原因になっているわけです。
ではこのとき電場から受ける力はどのように表されるのかを考えて見ましょう。
まず、地球表面の重力場から受ける力を表す式を考えます。
ご存知のとおり、
重力場から受ける力=物体の質量m×重力加速度g
と表されます。
これを場という考え方で見て意味づけすると、
・質量mは、重力場が生じた原因の質量に対応している物理量
・重力加速度gは、どんな質量の物体でも共通なものなので、重力場の状態を表している値
と考えることができます。
これらを一般的にまとめると、
場から受ける力
=場が生じた原因に対応している物理量×場の状態を表す物理量 (*)
とみなすことができます。
このことをふまえて、電場を重力場の類推でとらえてみましょう。
まず、質量mに対応するものは電気量qです。
重力場の原因は質量であり、電場の原因は電気が帯びていることだからです。
よって、次の対応関係が成り立ちます。
質量m ⇔ 電気量 q
重力場において場の状態を表す物理量は重力加速度gです。
ここで、電場において場の状態を表す物理量を電場Eと定義します。
そうすると、次の対応関係が成り立ちます。
重力場の状態g ⇔ 電場 E
以上より、(*)をふまえて、
電場から受ける力F=電気量q×電場E
と電場から受ける力が表されると類推できます。
電場Eの定義
電場Eの値はどうやって定義し、その物理量を求めることができるのでしょうか。
重力場と対応させて考えていきます。
重力場において、+1Kgの物体に注目すると、F=mgより、
F=+1×g ⇔ F=g
つまり、
(+1Kgの物体が受ける力の大きさと向き)=(重力加速度の大きさと向き)
となり、重力場の状態を表す重力加速度を求めることができます。
同様にして、 電場において、+1Cを帯びている物体に注目すると、F=qEより、
F=+1×E ⇔ F=E
つまり、
(+1Cの受ける力の大きさと向き)=(電場の大きさと向き)
となり、電場を定義し、求めることができるようになります。
定義を使って求めなくてはいけません。
電場の位置エネルギーと電位Vの定義
重力場において、物体は重力場による位置エネルギーをもちます。
同様に、電場においても物体は電場による位置エネルギーをもちます。
地球表面の重力場と対応させて考えると、次のように電場の位置エネルギーを考えることができます。
重力場による位置エネルギーU⇔ mgh=質量m×g×位置
電場による位置エネルギーU ⇔ 電気量q×E×位置(☆)
(∵質量m ⇔ 電気量 q 、重力場の状態の大きさg ⇔ 電場の大きさE)
一般に、電場の大きさEは位置により変わるので、
電場の大きさEと位置をいっしょに考える(基準量とする)ことにします。
このときの基準量を電位V(つまり、E×位置=電位V )とすると、
電場による位置エネルギーU=電気量q×電位V となります。
電位Vの定義は、電場の定義のやり方と同じように+1Cを帯びている物体に注目すると、
U=+1×V ⇔ U=V
となることより、
(+1C の持つ電場によるエネルギー)=(電位Vの大きさ)と表されます。
まとめ
- ある空間にいるだけで物体に必ず働く力を場の力という
- 電場の概念は地球表面の重力場による力:F=mgと対応させると分かりやすい
- 電場による位置エネルギー、電位の概念は地球表面の重力場の位置エネルギー:U=mghと対応させると分かりやすい
投稿者 doraneco5675 : 06:06
2004年12月12日
運動方程式の変形
目次
目標
力学の問題を解くとき中心となる法則は、運動方程式、力学的エネルギー保存則、運動量保存則です。
しかし、どんなケースのときにどの法則を使えばよいのかを、よく分かっていない人も多いのではないでしょうか。
実は、これらの3つの法則には次のようなつながりがあります。
力さえわかれば、運動方程式を解くことによってどんな運動でも解析できる。
しかし、必ずしも力を求めることができないので、力がわからなくても式を立てることができる力学的エネルギー保存則、運動量保存則に変形する。
このことを知っていればわけもわからずに式を立てることは無くなります。
この記事の目標は、このつながりを意識して問題を解けるようにすることです。
すこし微積の話が出てきますが、わからない人はよくわからないけど結果そうなるんだなぐらいの理解で十分です。そのうち分かるようになります。
力学の問題の解き方
物体の任意の時刻での位置を求めることが力学の目的です。
位置を求めるためには、速度、加速度の情報が必要です。
微分の逆操作が積分なので、
加速度が分かれば、時間で積分することにより速度が分かります(v=∫adt)。
速度がわかれば、時間で積分することにより位置が分かります(r=∫vdt)。
(積分をするときは初期条件がないと値が確定しない)
加速度は「運動方程式 ma=F」から求めることができるので、
原理的にはどんな問題でも運動方程式を立てれば必ず解くことができるはずです。
「運動方程式」の問題と対応策
「運動方程式」は微分が含まれた方程式なので、数学の言葉では微分方程式といいます。
この微分方程式を解けば、位置、速度、加速度が求まります。
しかし、「運動方程式」には問題があります。
力を具体的な関数で表せなくては「運動方程式」を解くことができないのです。
このようなとき、問題を解くために運動方程式を変形する必要があります。
これからその変形の2つの方法を解説します。
- 保存力・・・位置の関数
- 平面上の運動の抗力・・・定数
- 傾角θの斜面上の運動の抗力・・・定数
- 曲面上の運動の抗力
- 振り子の張力
「運動方程式」に仕事の定義を適用する
最初に準備として、仕事の定義について説明します。
物理での仕事Wは、力Fと変位Δrの内積で表されます。
厳密に定義すると次のようになります。
点Aから点Bにある軌道に沿って移動したときの仕事:
W=∫軌道F・dr(点A→点B)
それぞれの微小仕事dW(=力Fと微小変位drの内積=F・dr)を求め、それらを足しあわせる(∫軌道dW)ことを表しています。
軌道に沿った積分は大学で学ぶ範囲です。
仕事の定義式を見ると力、軌道が含まれているので、
仕事を求めるためには力の関数、軌道の関数を求めなくてはならないことが感覚的に分かると思います。
しかし、簡単に仕事が求めることができるケースがあります。
・力が0のとき
・力と変位が常に直交するとき
です。
1つ目のケースは本当に簡単ですね。
力が0なのだから、仕事が0になるのは当然です。
2つ目のケースをこれから解説します。
力と変位が常に直交しているので、微小に変位しているときも力と変位は直交しています。
このとき、微小仕事dW=F・dr=Fdr cos90°=0(∵cos90°=0)となり微小に変位したときの仕事は常に0なので、トータルの仕事Wも0になります。
このように、常に力と変位が直交しているときは、力の関数がわからなくても簡単に仕事の値は0と求めることができます。
これらの仕事の性質は後の話で役に立つので覚えておいてください。
ここから、「運動方程式」の変形の1つ目の方法:「運動方程式」に仕事の定義を適用 を紹介します。
仕事の定義の形にするために、運動方程式の両辺を位置で積分すると、
(移動前の運動エネルギー)+(移動間の仕事)=(移動後の運動エネルギー)
となります。これはエネルギーの原理と呼ばれています。
x軸上を常に一定の力Fxを受けて動く等加速度運動の場合で考えます。
(xAからxBに移動したとする)
運動方程式の両辺を位置xで積分すると、
∫m ax dx=∫Fxdx ← 右辺が仕事を表す
(xの積分区間:xAからxB)
このとき、
(左辺)=m ax ∫dx ← m,axは定数だから外に出した
=m ax Δx ← ∫dx=xB-xA=Δx
等加速度運動の公式
vB2 - vA2=2 ax Δx
を代入すると、
(左辺)=m(vB2 - vA2)/2
=(1/2)mvB2 - (1/2)mvA2
を得る。
以上より、運動方程式を位置で積分したとき、
(1/2)mvB2 - (1/2)mvA2=W
⇔(1/2)mvA2+W=(1/2)mvB2
⇔(移動前の運動エネルギー)+(移動間の仕事)=(移動後の運動エネルギー)
となることが分かる。
積分を使った一般的な議論は、微積を使って力学の世界を見るで解説します。
移動間に働く力を保存力(重力、弾性力など仕事の値が軌道によらないで最初と最後の位置で決まる力)と非保存力(保存力でない力)に分類すれば、
(移動間の仕事)=(移動間の保存力の仕事)+(移動間の非保存力の仕事)
と変形できます。
ここでいきなりですが、
物体に働いている力が保存力のとき、現在の位置から適当に選んだ任意の基準点の位置までに運んだときに保存力がする仕事を位置エネルギーと定義します。
位置エネルギーの定義から、
(移動前の位置エネルギー)=(移動前の位置から基準点までの保存力の仕事) (1)
(移動後の位置エネルギー)=(移動後の位置から基準点までの保存力の仕事) (2)
(1)-(2):
(移動前の位置エネルギー)-(移動後の位置エネルギー)=
(移動前の位置から基準点までの保存力の仕事)-(移動後の位置から基準点までの保存力の仕事)
⇔(移動前の位置エネルギー)-(移動後の位置エネルギー)=
(移動前の位置から基準点までの保存力の仕事)+(基準点から移動後の位置までの保存力の仕事)(∵-(AからBまでの仕事)=+(BからAまでの仕事))
ここで、右辺は(移動前の位置から移動後の位置までの保存力の仕事)を表しているといえるので、
(移動後の位置エネルギー)-(移動前の位置エネルギー)=(移動間の保存力の仕事)
これらの式をエネルギーの原理に代入すれば、
{(移動前の運動エネルギー)+(移動前の位置エネルギー)}+(移動間の非保存力の仕事)
={(移動後の運動エネルギー)+(移動後の位置エネルギー)}
と変形されます。
この式で値を求めるのが難しそうなのは、移動間の非保存力の仕事です。
非保存力の関数が分からないと求めることができないからです。
「これでは運動方程式のときと同じなのでは?」と思うかもしれません。
しかし、運動方程式に仕事の定義を適用した形で考えると、
非保存力の部分が消える都合のよいケースが起きます。
そのケースとは、非保存力が0または非保存力と変位が常に直交しているときです。
最初に解説したように、どちらのケースでも仕事の値は0になります。
よって、このときのエネルギーの原理は、
{(移動前の運動エネルギー)+(移動前の位置エネルギー)}
={(移動後の運動エネルギー)+(移動後の位置エネルギー)}
となります。 この式は力学的エネルギー保存則と呼ばれています。
・非保存力が0
または、
・非保存力と変位が常に直交
であることが分かります。
力学的エネルギー保存則の形に変形すれば、運動方程式のままでは何の情報も得られなかった式から物体の情報の一部を取り出すことができます。
- 曲面上の運動の垂直抗力
- 振り子の張力
- 摩擦のない曲面上の運動
- 振り子運動
「運動方程式」に力積の定義を適用する
<その1>では運動方程式を位置で積分しました。
<その2>では運動方程式を時間で積分する事を考えます。
先ほど解説したように、力と変位の積は仕事です。
力と時間の積で表される物理量もあって、力積と呼ばれます。
時刻tAからtBの間に働く力積は、
∫Fdt(tの積分区間:tAからtB)
と定義されています。
仕事では値が0になるケースがありましたが、力積も0になるケースがあります。
・力が0の場合
・力が働いていたのが瞬間的だった場合
です。
いつでも瞬間的なら力積は0というわけではないことに注意してください。
たとえば、衝突は瞬間的ですが、衝突前後で速度は変わりますよね。
速度が変わるということは、瞬間的な衝突をしたときに働いている力(撃力)による力積は無視できないということです。
では、「運動方程式」の変形の2つ目の方法:「運動方程式」に力積の定義を適用 を紹介します。
力積の定義の形にするために時間で積分すると、運動方程式は、
(質量)×(力が加わる前の速度)+(力が加わっている間の力積)
=(質量)×(力が加わった後の速度)
と変形できます。これは運動量の原理と呼ばれています。
x軸上を常に一定の力Fxを受けて動く等加速度運動の場合で考えます。
(時刻tAからtBの間に、xAからxBに移動したとする)
運動方程式の両辺を時間で積分すると、
∫m ax dt=∫Fxdt ←右辺は力積を表している
(左辺)=m ax∫dt←定数を外に出した
=m axΔt ←∫dt=tB-tA=Δt
加速度axは一定なので、
ax=dvx/dt=Δv/Δt ←瞬間の速度=平均の速度
が成立する。
よって、
(左辺)=m(Δv/Δt)Δt=mΔv
=m(vB-vA)
=mvB-mvA
を得る。
よって、運動方程式を時間で積分したとき、
mvB-mvA=∫Fxdt
⇔mvA+∫Fxdt=mvB
⇔(質量)×(力が加わる前の速度)+(力が加わっている間の力積)
=(質量)×(力が加わった後の速度)
となることが分かる。
積分を使った一般的な議論は、微積を使って力学の世界を見るで解説します。
これを利用すると、運動方程式では解けない(もしくはめんどくさい)現象を見ることができます。
以下ではその具体的な例として、2つの物体の空中での衝突を考えます。
2つの物体が衝突すると、2つの物体が衝突する瞬間に撃力とよばれる非常に大きい力が働きます。
この力を具体的に知る事はできないため、運動方程式のままでは対応ができません。
そこで、衝突の現象に運動量の原理を適用してみましょう。
2つの物体をA,Bとして、運動量の原理を使うと、
Aについて、
(Aの質量)×(Aに力が加わる前の速度)+(Aに力が加わっている間の力積)
=(Aの質量)×(Aに力が加わった後の速度)
Bについて、
(Bの質量)×(Bに力が加わる前の速度)+(Bに力が加わっている間の力積)
=(Bの質量)×(Bに力が加わった後の速度)
が成立します。
この2つの式を足せば、
(Aの質量)×(Aに力が加わる前の速度)+(Bの質量)×(Bに力が加わる前の速度)
+{(Aに力が加わっている間の力積)+(Bに力が加わっている間の力積)}
=(Aの質量)×(Aに力が加わった後の速度)+(Bの質量)×(Bに力が加わった後の速度)
となります。
力積の定義とA,Bの衝突時間が等しいことに注意して赤色の部分を変形すると、
赤色の部分={(Aに働く力)+(Bに働く力)}×(衝突時間)
となります。
衝突の瞬間に働く力は、
(Aに働く力)=(BがAに及ぼす撃力)+(Aに働く重力)
(Bに働く力)=(AがBに及ぼす撃力)+(Bに働く重力)
です。
よって、
(Aに働く力)+(Bに働く力)
=(BがAに及ぼす撃力)+(Aに働く重力)+(AがBに及ぼす撃力)+(Bに働く重力)
={(BがAに及ぼす撃力)+(AがBに及ぼす撃力)}+(Aに働く重力)+(Bに働く重力)
となります。
撃力は物体間で働く力(=内力)なので、作用・反作用の法則より、
{(BがAに及ぼす撃力)+(AがBに及ぼす撃力)}=0となります。
よって、撃力による力積はA,Bを合わせて考えると、トータルで0になります。
ただし、Aに働く撃力による力積、Bに働く撃力による力積が0になっているわけではありません。あくまでA,Bを合わせて考えるとちょうど打ち消しあっているだけです。
次に、重力による力積が瞬間的なため0と近似できるという話が出てきますが、撃力はとても大きい力なのでたとえ瞬間的でもその力積を0とすることはできません。
このとき、
赤色の部分
={(Aに働く重力)+(Bに働く力)}×(衝突時間)
=(Aに働く重力)×(衝突時間)+(Bに働く力)×(衝突時間)
となります。
この2つの項は、A,Bの重力による力積なのですが、
衝突時間が瞬間的なので0と近似することができます。
結局、赤色の部分=0となるので、2つの物体の運動量の原理の式をたし合わせたものは、
(Aの質量)×(Aに力が加わる前の速度)+(Bの質量)×(Bに力が加わる前の速度)
=(Aの質量)×(Aに力が加わった後の速度)+(Bの質量)×(Bに力が加わった後の速度)
となります。この式は運動量保存則と呼ばれています。
・物体間に働く力以外の力(=外力)が0
または、
・衝突が瞬間的で外力による力積が無視できるとき
であることが分かります。
運動方程式を変形した運動量保存則を衝突現象に使うと、衝突時の力が消えるため衝突の問題を解くことができます。
まとめ
- 力学の問題は、運動方程式、力学的エネルギー保存則、運動量保存則を使って解く
- 運動方程式は力の関数を求めなければ解けない
- 力学的エネルギー保存則、運動量保存則に変形すると、なんらかの情報を取り出すことができるケースがある
- 力学的エネルギー保存則は、非保存力が0 または 非保存力と変位が直交するとき成立する
- 運動量保存則は外力が0 または 衝突が瞬間的で外力による力積が無視できるとき成立する
更新履歴
08/05/06 エネルギーの原理のなかの位置エネルギーの式(1),(2)の符号が逆になっていたのを訂正。投稿者 doraneco5675 : 20:08
2004年12月06日
物理のための微積
目次
目標
微積は物理を定量的(→現象を量で表す)に理解する道具です。
単純な現象のときは、量の変化も単純なので量の変化を表す(微積の準備)で紹介した変化量、平均変化率だけで処理できます。
しかし、複雑な現象になると、微積を使わないと正しく量の変化を表すことができません。
このため、物理を厳密に理解するためには微積が必要不可欠だと言えます。
しかし、微積に慣れていない普通の高校生にとって、微積をどうやって物理に使うのかよくわからないと思います。
そこで、微積にあまり慣れていない人を対象に、物理の世界を理解するのに役立つ直観的な微積の考え方を解説します。
最後のほうで少し微積を使って物理の問題を解くための計算方法についても紹介します。
微積のポイント
微積の考え方の一番重要なポイントをまとめます。
微積の意味がわからない人にはピンと来ないかもしれませんがとりあえず頭に入れてください。
微積とは、微小区間(無限に細かい区間)で考えること。
微小区間では、
・関数の「変数」を「定数」
・図形の「曲線」を「直線」
と近似できる。
ある変数が微小に変化したとき、他の変数の変化はほとんど0に近いので、他の変数の変化は無視して定数とみなそうということです。 当たり前ですが、微小変化まで変化してないとみなしたら何も変化しないことになってしまい意味がなくなります。
□「曲線」を「直線」と近似できるとは
私たちが実感できる例があります。
地球は丸いですね。でも私たちにとって地面は平面に見えます。
これは私たちの見ることができる範囲が、地球の大きさに対してはるかに小さい(微小)からです。
つまり、どんな曲線でもすごく小さい範囲に限定すると直線とみなせるわけです。
これが微積の考え方のエッセンスです。
これから微分の考え方と積分の考え方について詳しく解説していきます。
| 普通の世界 | 微小の世界 | |
| 関数 | 変数 | 定数 |
| 図形 | 曲線 | 直線 |
| 直接計算できない | 直接計算できる |
微分の考え方
微分とは、ある点での変化率、曲線の接線の傾き(直接計算できない)を
平均変化率、直線の傾き(直接計算できる)とみなすことです[表2]。
| 普通の世界 | 微小の世界 | |
| 関数 | ある点での変化率 | 平均変化率 |
| 図形 | 曲線の接線の傾き | 直線の傾き |
| 直接計算できない | 直接計算できる |
微分の考え方が物理に使われていることを、物理量:瞬間の速さを定義することを通して考えていきます。
まず、中学生のときに学んだ速さの定義を確認しましょう。
速さの定義(中学生版):
(時刻t から時刻t+⊿t までの間の速さ)
=(位置の変化量)/(時間の変化量)
文字式で書くと、v = Δr/Δt -(*)
となります。
位置の変化量と時間の変化量がわかれば、この定義式により時刻tから時刻t+⊿tまでの間の速さを求めることができます。
では、瞬間の速さの定義もこの定義(*)を使えばよいのでしょうか?
ちょっと考えてみると、この定義式(*)を瞬間の速さの定義とするには無理があるのに気づきます。
たとえば、10kmを2時間(時刻t から時刻t+2 の間)で走ったとしたら、
速さの定義式(*)により、速さ=5Km/hと求まります。
しかし、2時間走っていて、全ての瞬間で速さが5Km/hとは限らないのではないでしょうか?
ある時刻では休んでいたり、また別の時刻では普段より速く走っているかもしれません。
つまり、(*)の速さの定義式は2時間走ったときの平均の速さを意味していて、走っている間の すべての瞬間の速さを表してはいないのです。
一般的に言い直すと、(*)の速さの定義は時刻t から時刻t+⊿t までの間の時間⊿tの平均の速さであり、時間⊿tの間の全ての時刻での瞬間の速さを表わしてはいない、ということです。
では、このとき瞬間の速さ、たとえば時刻t での瞬間の速さを定義するにはどうすればよいのでしょうか?
上の例で時刻tでの瞬間の速さを求める事ができなかったのは、
速さを測定する時間が⊿t=2時間と長かったため、時刻tでの瞬間の速さから値のずれが大きくなってしまったためと考えられます。
逆に考えれば、速さを測定する時間を小さくすれば瞬間の速さからの値のずれが小さくなり、瞬間の速さに近づくのではないでしょうか。
そこで、瞬間の速さを、平均の速さの定義で測定時間⊿tを限りなく小さくにしたものと定義します。
式で書くと、
瞬間の速さの定義:
瞬間の速さv = limΔt→0 Δr/Δt = dr/dt -(*')
となります。
Δ●→0のときΔ●はd●と表わします。このとき、●に依存する変化量Δ■もd■と表します。
これはある点での変化率は微小区間の平均変化率に一致するという微分の考え方です。
ここまでは瞬間の速さを関数的に考えてきました。
ここからは図形的意味を考えます。
まず準備として、平均の速さΔr/Δtの図形的意味を考えてみましょう。
rとtの関数が[図1]のようになっているとき、平均の速さ:Δr/Δtは点A(時刻t)と点B(時刻t+Δt)を通る直線の傾きを表します。
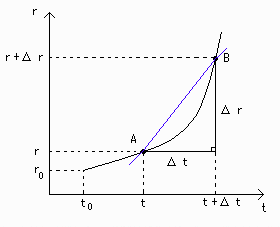
[図1] Δr/Δtの図形的意味
特に、速さが一定のときは、
v=Δr/Δt (=一定)に(t0,r0)と(t,r)を代入して、
v=(r-r0)/(t-t0)
⇒ r=v(t-t0) + r0
となり、rとtの関数は直線になるので、
(rとtの関数の直線の傾き)=(直線ABの傾き)=(速さ)
となります。[図1']
(速さが一定のとき、Δr/Δtは物理的意味を持つ)
これは瞬間の速さを図形的に見るときの伏線になっています。
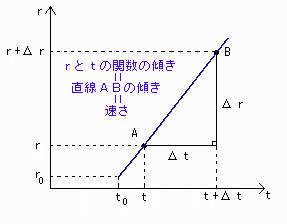
[図1'] 速さvが一定のときのΔr/Δtの図形的意味
ここから瞬間の速さの図形的意味を考えていきます。
瞬間の速さを求めるために測定時間Δtを0に近づけると、
[図2]のように点BはB0→B1→B2→・・・→Bn→・・・と点Aに近づいて行き、最終的に点Aと点Bはほとんど同じ点になります[図2]。
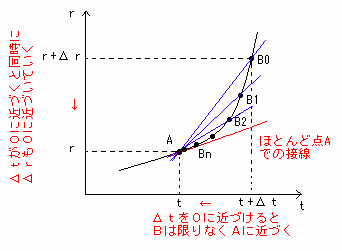
[図2] Δtを0に近づける
このとき、点Aの付近を見てみると、点Aと点Bの間隔が微小になっているため、
rとtの関数の曲線は点AB間で直線に近似でき直線ABと一致しています[図3]。
これは[図1']の状況と同じですよね。
ですから、このときの直線の傾きは瞬間の速さを表しています。
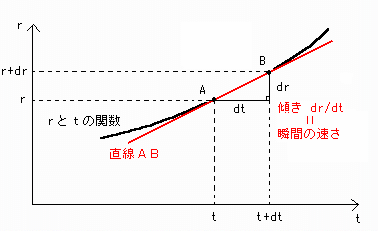
[図3] 点A付近の拡大図
[図3] は点A付近を非常に拡大して見ているので、点Aと点Bは離れているように見えます。
しかし、普通の世界では点Aと点Bはほとんど一致しているので、直線ABは点Aでの接線です。
以上より、瞬間の速さv = limΔt→0 Δr/Δt = dr/dt -(*')の図形的意味は、
r-tグラフの接戦の傾きであると分かりました。
これはある点での接線の傾きは微小区間の直線の傾きに一致するという微分の考え方です。
Δとdの違い
Δ●とd●はどちらも●の変化量を表しています。
Δとdの違いは変化量の大きさにより決まります。
変化量が数値で表せるぐらい大きいときは、Δ●と書き、
変化量が数値で表せないくらい微小なときは、d●と書きます[図4]。
[図4] Δとdの違い
図形的には、Δが測定できる幅を持っているのに対して、
dは幅が測定できないくらい微小で私たちにとって点にしか見えない。
Δとdの違いをふまえれば、
次の2つの運動方程式
m(d2r/(dt)2)=F -(*) と m(Δ2r/(Δt)2)=F -(**)
の違いが見えてきます。
(*)は、私たちには感じられないくらい微小な時間の変化の間(時刻tからt+dt)の運動方程式なので、ある瞬間(時刻t)の運動方程式とみなすことができます。
一方(**)は、時間の変化量がΔtなので、この式は瞬間ではなく一定の時間の間(時刻tからt+Δtの間)での運動方程式を平均したものと考えられます。[図5]
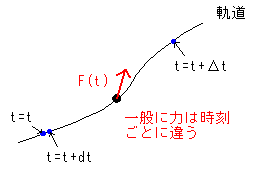
[図5] 運動方程式でのΔとdの違い
d●は必ず微小量の変化を表します。
Δもdも「差」を表していますが、dは日常の概念を超えた「差」を表していることを意識しましょう。
積分の考え方
変数、曲線を無限個の微小な区間に分け、
変数に依存する変化量、曲線で囲まれた図形の面積・体積(直接計算できない)を、
変数に依存しない変化量、直線で囲まれた図形の面積・体積(直接計算できる)の集まり
としてとらえるのが積分です[表3]。
[表3] 積分の考え方
| 普通の世界 | 微小の世界 | |
| 関数 | 変数に依存する 変化量 | 変数に依存しない(定数) の変化量の集まり |
| 図形 | 曲線で囲まれた 面積・体積 | 直線で囲まれた 面積・体積の集まり |
| 直接計算できない | 直接計算できる |
積分の考え方が物理に使われていることを、物理量:移動距離を求めることを通して考えていきます。
まずは、中学で習う方法で考えて見ます。
速さの定義(中学版)・平均の速さ(*)は
Δr = vΔt -(**)
と変形できます。
この式により、速さと時刻の変化量がわかれば移動距離を求めることができます。
たとえば、つねに時速5Km/hで2時間走ったとき、移動距離は(**)より10Kmと求めることができます。
しかし、この式には問題があります。
速さが時刻により変わるとき、どの時刻の速さを代入すればいいのでしょうか?
(**)は平均の速さの式を変形したものなので、ここに代入できるのは一定の速さ(平均の速さは一定)だけなのです。
移動中のどの瞬間の速さでも使えますが、一般的に成立することではありません。
では、一般的に移動距離(時刻tからt+Δtの間移動したとする)を求めるにはどうすればよいのでしょうか?
(**)の式を使って移動距離を求めることができないのは、時間が経過するとともに速さが一定ではなくなるためです。
この問題は、移動時間を無限小な時間に分け、微小な時間ごとに移動距離を求めることによって解決できます。
なぜなら、無限小な時間では速さは瞬間の速さとなり定数とみなせる(ある一瞬の速さだから値は変わらない)からです。
瞬間の速さは定数だから、平均の速さの式(**)から微小時間の間の移動距離を求める事ができます。
それを時刻tからt+⊿t までたし合わせれば全体の移動距離になります。
1秒の間に速度は変わるかもしれませんが、30分の平均速度を使うよりは、正確な移動距離が出そうですよね。1秒よりもっと微小に分ければ、もっと正確な値が出てきます。
式で書くと、
速度が一定でないときも含む移動距離の定義:
微小時間dtの間の移動距離dr= vdt (瞬間の速さの定義より)
時間⊿t の間の移動距離Δr = ∫dr (区間:r(t0)→r(t0+⊿t)) = ∫vdt (区間:t0→t0+⊿t) -(***)
となります。
数列でのΣに対応しています。
Δ●=∫d● (区間:変化前の値→変化後の値)と表されます。
この式は、●の微小変化を集まれば●の変化量となることを意味しています。
これはある区間で変数に依存する変化量を、
区間を微小区間に分けて考えることにより、
変数に依存しない変化量の集まりとみなす
という積分の考え方です。
ここまでは移動距離を関数的に考えてきました。
ここからは図形的意味を考えます。
瞬間の速さのときはr-tグラフを書きましたが、移動距離ではv-tグラフを書きます。
vとtの関数は[図6]にあるように時刻とともに増加していくケースを考えます。
先ほど、Δr = vΔt -(**) は速度一定のときにしか使えないと解説しました。
このことを図形的に確認してみましょう。
(**)に点A(時刻t0)のときの速さv0を代入すると、
Δr = v0Δt となります。
これは[図6]の青色の四角形の斜線部分の面積ですが、速さが変わるときの移動量距離を表していないことは明らかです。
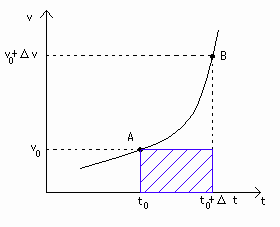 [図6] vΔtの図形的意味
[図6] vΔtの図形的意味
特に、速さが一定のときは、
移動距離Δr = vΔt (v=一定)
⇒ Δr = vΔt(直線)となり、これは[図6']の斜線部分の面積(vとtの直線とt軸を含む四角形の面積)なるので、
(vとtの関数の直線とt軸を含む四角形の面積)=(時間Δtの間の移動距離)-(☆☆)
となります。
(速さが一定のとき、vΔtは物理的意味を持つ)
これは移動距離を図形的に見るときの伏線になっています。
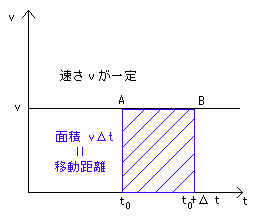
[図6'] 速さが一定のときのvΔtの図形的意味
ここから速度が一定でないときの移動距離の図形的意味を考えていきます。
移動距離を求めるとき、微小時間ごとに移動距離を求めます。
[図7]のように、微小時間dtを取ると、時刻tの付近ではvとtの関数は斜めの直線に近似することができます。
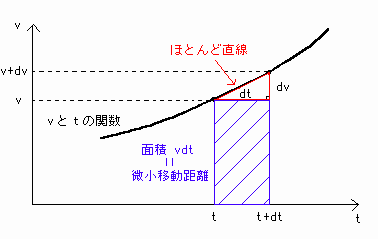
[図7] vdtの図形的意味
このとき、dr = vdt -(**')は、青色の四角形の面積を表します。
実はdr = vdtは青色の四角形の面積であり赤色の三角形を含んだ台形の面積でもあるのです。
日常感覚では理解できませんが、微小な世界では許される話なのです。
実際に、台形の面積を求めると、{v+(v+dv)}dt÷2=vdt+dvdt
でdvdtは微小な数同士の積なので0と近似してよく、結局台形の面積はvdtとなっています。
青色の四角形と赤色の三角形を含む台形の面積が等しいということは、
微小な面積を考えるとき、微小区間dtでvはほとんど一定とみなしてよいということです。
つまり、先ほどvとtの関数は斜めの直線に近似と言いましたが、実際にはほとんど傾きが0の直線に近似されるのです。
これは[図6']の状況と同じなので、vdtの物理的意味は微小時間dtの間の移動距離といえます[図7]。
これより、時間⊿t の間の移動距離Δrの図形的意味が分かります。
定義より、
Δr = ∫dr (区間:r(t0)→r(t0+⊿t))
= ∫vdt (区間:t0→t0+⊿t) -(***)
と表されます。
vdtは微小時間の移動距離であり、v-tグラフにおいて微小な四角形の面積を表しているので、
∫vdt (区間:t0→t0+⊿t)の図形的意味はvとtの関数とt軸で囲まれる部分の面積と分かりました[図8]。
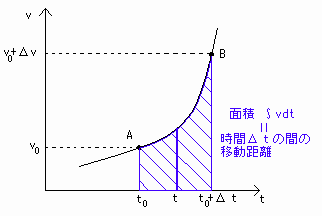
[図8] ∫vdtの図形的意味(区間:t0→t0+⊿t)
このように、微小区間に注目して、
まず微小変化量を求め、
それを足し合わせて全体の変化量を求めることを、
数学の言葉で積分といいます。
微積を使って物理を見る(初心者向け)
今までやってきたことをポイントにまとめます。
今までの話がよくわからなかった人もとりあえずここだけは押さえておきましょう。
- ある▲に対する●の変化率を表す
- ●-▲グラフの接線の傾き
(例)v =dx/dt(■=v(速度)、●=x(位置)、▲=t(時刻))のとき
- あるtに対するxの変化率⇔ある瞬間のxの変化率⇔瞬間の速度
- x-tグラフの接線の傾き
- ●の変化量(区間:●→●+⊿●)
- ■-▲グラフの面積(区間:▲→▲+⊿▲)
(例)∫dx =∫vdt (区間:x0→x0+⊿x、t0→t0+⊿t) (■=v(速度)、●=x(位置)、▲=t(時刻))のとき
- 位置の変化量(区間:x0→x0+⊿x)
- v-tグラフの面積(区間:t0→t0+⊿t)
微分の定義式:■=d●/d▲から求まる微小変化:d●=■d▲を足し合わせることによって求まる。
微積の計算を具体的にしない場合でも、上のポイントは知っておくと、
微積で表わされている式から、グラフの接線の傾きや面積がどんな物理的意味を持っているかが分かります。
たとえば、高校の教科書には電流の定義式:I =ΔQ/Δtとあります。
電荷Qは時刻によって変わる可能性があるので、一般的にはI =dQ/dtと微分を使って表さなくてはいけないことはもうわかりますよね。
上のポイントをふまえれば、微分の意味から、
- ある瞬間の電気量Qの変化率
- Q-tグラフの接線の傾き
また、I =dQ/dt ⇔ 微小変化:dQ =Idtより、
全体の変化:ΔQ = ∫dQ=∫Idt(区間が与えられているとする)が求まります。
この式は積分の意味から、
- ある区間での電気量Qの変化量
- ある区間でのI-tグラフの面積
・力学
速度v =dr/dt
加速度a =dv/dt
仕事W = ∫dW = ∫F・dr
仕事率dW/dt = F・dr/dt
運動量(力積)P = ∫dp = ∫Fdt
・熱力学
気体がする仕事WOUT= ∫dWOUT = ∫PdV
・電磁気
電流I = dQ/dt
電位差V = ∫dV = ∫E・dr
誘導起電力 V = -dΦ/dt
微積を使って問題を解く(上級者向け)
微積を使って力学の問題を解きます。
見慣れていないので複雑に見えると思いますが、高2で習うの微積と合成関数の微分を知っていれば理解できます。
数式を追うだけでなく、物理的意味を考えながら読んでみてください。
(1)物体の運動を求めよ。
(2)物体のエネルギー保存則を導け。
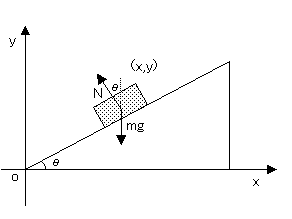
以下では、d●/dt=●'、d2●/dt2=●"と表す。
<解答>
(1)
図のように地面に平行な方向にx軸、垂直な方向にy軸を取る。
・運動方程式
mx"(t)=-Nsinθ (1)
my"(t)=Ncosθ-mg (2)
・初期条件
x(0)=0,y(0)=0 (3)
x'(0)=v0cosθ,y'(0)=v0sinθ (4)
・束縛条件
tanθ=y(t)-y(0)/x(t)-x(0)(物体は常に斜面上にある) [t≠0]
⇒y(t)=tanθx(t) (5) [t=0も含む]
目標:時刻tでの物体の位置(x(t),y(t))を求める。
(1)*cosθ+(2)*sinθよりNを消去:
mx"(t)cosθ+my"(t)sinθ=-mgsinθ
⇔x"(t)cosθ+y"(t)sinθ=-gsinθ (6)
(5)を2回時間微分する:
y"(t)=tanθx"(t) (7) ※d●/dt=●',d●'/dt=●"
(6),(7)よりy"(t)を消去:
x"(t)cosθ+tanθsinθx"(t)=-gsinθ
⇔x"(t)/cosθ = -gsinθ
∴x"(t)=-gsinθcosθ
また、(7)より、y"(t)=-g(sinθ)2
x"(t)=-gsinθcosθと初期条件(3),(4)より、
x'(t)=-gsinθcosθt+v0cosθ
※∫d●=●+C(積分定数) 、初期条件よりC=v0cosθが決まる
x(t)=-(1/2)gsinθcosθt2+v0cosθt
※∫●+C d●=(1/2)●2+C●+D(積分定数) 、初期条件よりD=0が決まる
y"(t)=-g(sinθ)2と初期条件(3),(4)より、
y'(t)=-g(sinθ)2t+v0sinθ
y(t)=-(1/2)g(sinθ)2t2+v0sinθt
(2)
エネルギー保存則を求めます。
運動方程式の両辺に速度をかけると、
(1)*x'(t)+(2)*y'(t) ※仕事率dW/dt=F・V=Fx*Vx+Fy*Vy :
mx"(t)x'(t) + my"(t)y'(t) =-Nsinθx'(t) +Ncosθy'(t) -mgy'(t)
⇔d/dt( (1/2)mx'(t)2+ (1/2)my'(t)2 ) ※d/dt(●2) = 2●●'
= N(-sinθx'(t) +cosθy'(t)) - mgy'(t)
さらに、(5)より-sinθx'(t) +cosθy'(t)=0 ,d/dt(y)=y'より、
⇔d/dt( (1/2)mx'(t)2+ (1/2)my'(t)2 + mgy(t) ) = 0
この式は全ての時刻でエネルギーが一定であることをを表している。
つまり、エネルギー保存則を表す式である。
参考文献
- 図解雑学 微分・積分、図解雑学 わかる微分・積分
0から学ぶ入門書として最適 - 細野真宏の数IIIの微分積分が面白いほどわかる本(微分編)
微分の意味について Section1微分の定義に解説があります。 - 細野真宏の微分積分(原則編)・軌跡が面白いほどわかる本
積分の意味について、1.3.(1)体積の考え方(積分とは?)に解説があります。
投稿者 doraneco5675 : 21:07
2004年12月04日
束縛条件の求め方
物体はあらゆる値の位置、速度、加速度をとることができます。
しかし、何らかの制限を受けて位置、速度、加速度はとることができる値を制限される場合があります。
このときの物体の運動を束縛運動といい、その束縛運動を決める条件を束縛条件と呼びます。
高校物理の範囲の運動は、単純なものが多いので普段は束縛条件を意識することがありません。
しかし、束縛条件なしに束縛運動は解けないので、この機会に知っておきましょう。
入試問題で複雑な状況設定が出てきたときに役立ちます。
ここでは具体的な問題を通して束縛条件について考えて行きます。
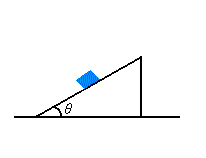
解答は、
斜面に水平方向:m a = mg sinθ
斜面に垂直方向:m 0 = N - mg cosθ⇔ N = mg cosθ(N:垂直抗力)
となります。
よくある設定なので解答を覚えてしまっている人もいるかもしれませんが、この解答に束縛条件が使われています。わかりますか?
上の解答では、本来任意の値を取ることができる加速度について、斜面に水平方向をa、斜面に垂直方向を0と勝手に決めてしまっています。
このように加速度のとることができる値を制限するものが束縛条件なのです。
では、束縛条件はどのように求めるのでしょうか。
求め方をPointにまとめます。
Step1. 物体の運動を制限する条件を問題文から見つける。
Step2. 物体の運動が制限されるときにとる軌道を求める。
Step3. Step2.で求めた軌道を物体が運動するために、物体がとらなくてはならない位置、速度、加速度を求める。それが束縛条件となる。
このPointにしたがって、<問題>の束縛条件を求めましょう。
まずStep1です。
問題文を見ると、斜面上を動いているとあります。
本来、物体は斜面上だけを動く以外に、斜面から飛んだりする可能性などもあるわけだから、これは物体の運動を制限している条件です。
次にStep2です。
斜面上を動いているのだから、軌道は斜面に沿ったものになります。それ以外の軌道は取りません。
最後はStep3です。
このStepは定性的に求める方法と、定量的に求める方法の2通りのやり方があります。ここでは両方の方法で求めます。
●定性的に考える
斜面に沿った軌道を取ると言うことは、物体は常に斜面上に位置していて、斜面に沿った方向にしか物体は移動しません。
よって、斜面に沿った方向以外の加速度、速度の成分はゼロになります。
なぜなら、もし加速度、速度がゼロでなければ物体が斜面に沿った方向以外に動いてしまうからです(※)。
※ある方向に加速度を持つ→その方向に速度を持つ→その方向に物体が移動する
この関係は、加速度=⊿(速度)/⊿(時間)、速度=⊿(位置)/⊿(時間)
をふまえれば明らかです。
よって、束縛条件は
・位置・・・斜面上
・速度・・・斜面に沿った方向以外の速度の成分はゼロ
・加速度・・・斜面に沿った方向以外の加速度の成分はゼロ
となります。
●定量的に考える
斜面に水平な方向をx軸、垂直な方向をy軸とします。
物体は斜面に沿った軌道を取るので、位置は
x=時間に依存する変数 ←具体的な値は不明
y=0
と求まります。
つぎに、速度v= (vx,vy) =dr/dt = (dx/dt,dy/dt)より、速度は
vx = dx/dt = d(時間に依存する変数)/dt = 時間に依存する変数 または 定数
vy = dy/dt = d(0)/dt = 0
そして、加速度a= (ax,ay) =dv/dt = (dvx/dt,dvy/dt)より、加速度は
ax = dvx/dt = d(時間に依存する変数 または 定数)/dt = 時間に依存する変数 または 定数
ay = dvy/dt = d(0)/dt = 0
と求まります。
よって、束縛条件は
・位置・・・(x,0)
・速度・・・(vx,0)
・加速度・・・(ax,0)
(x,vx,axの具体的な値は不明)
となります。
このように求めた束縛条件を、運動方程式に代入すれば上の解答のようになるわけです。
束縛条件は、当たり前すぎることなので普段は意識しませんが、これを求めずに運動方程式を解くことはできないので、キチンと求めることができるようにして下さい。
ただ、定性的に求める方法は厳密性があまりないので、難関大学以上を目指す人は、定量的に求める方法を身につけたほうがよいでしょう。
微積を使うので難しく感じるでしょうが、やっていることは高2で習う簡単な微積です。
投稿者 doraneco5675 : 16:34
カオス
振動的外力を加えた減衰単振り子(長さl、質量m)の相空間を観察します。
外力の強さを変えることで、周期的運動またはカオス的運動を観察できます。
カオスの特徴として、系の状態を表す変数の初期状態でのわずかな違いが、時間と共に指数関数的に大きくなることがあげられます。
このため決定論的に記述される系であっても初期条件を完全に正確に知ることができない場合、後の時刻における系の状態を予測できなくなってしまいます。
このアプレットでは、
mld2θ/dt2+k dθ/dt+mg sinθ=Fcos(ωet)
を、無次元化したt'=t√(g/l)を用いて、
d2θ/dt'2+(1/Q)dθ/dt'+sinθ=Gcos(Ωt)
(1/Q:抵抗の強さ、G:外力の強さ、Ω:外力の角振動数を表す無次元のパラメータ)
ω=dθ/dt'
φ=Ωt'
と変形し、さらに整理した、
dω/dt'=-(1/Q)ω-sinθ+Gcosφ
dθ/dt'=ω
dφ/dt'=Ω
Q=2,Ω=2/3
を初期条件:(φ、θ、Ω)= (0,0,0)としてルンゲ・クッタ法で数値的に解くことにより、相空間(φ、θ、Ω)を描いています。
参考文献 計算物理学(慶應義塾大学物理学科3年)授業プリント
外力の強さを変えて相空間を観察する。徐々に運動に変化が起こります。
□ このアプレットからわかること
・G=0.9のとき、外力と同じ周期の周期運動
・G=1.15のとき、カオス的運動
・G=1.45のとき、外力の倍周期の周期運動
となる。
G=0.9やG=1.45のときの相空間の軌道に比べて、G=1.15のときの相空間の軌道は非常に複雑になっている。
投稿者 doraneco5675 : 14:28
波の伝播
波が媒質(青の点)を伝わっていく様子を観察します。また、角速度を自由に変えることができます。
波が伝播するとき、各媒質がどのように運動するかを観察する。
□ このアプレットからわかること
各媒質は垂直方向に振動しているだけで、波の進行方向である水平方向には移動していない。
軌道(Orbit)をonにして見ると、軌道が各媒質の垂直方向にしか残らことからわかる。
□ 課題
上の観察結果を定量的に考察する。
投稿者 doraneco5675 : 14:19
リサージュ図形
リサージュ図形の観察します。
水平(x)方向、垂直(y)方向の単振動の角振動数 ωx2 、ωy2を自由に変えることができます。
このアプレットでは、
水平(x)方向:m d2x/dt2 = - kx x ⇒ d2x/dt2 = - ωx2 x ( ωx2=kx/m)
垂直(y)方向:m d2y/dt2 = - ky y⇒ d2y/dt2 = - ωy2 y ( ωx2=ky/m)
初期条件:時刻t=0で(x,y)=(60,60),(vx,vy)=(0,0)
をオイラー法により数値的に解いています。
各成分の角振動数を変えてリサージュ図形を観察する。
また、各成分の角振動数の持つ物理的意味を考察する。
□ このアプレットからわかること
自分なりに書いてみる。
□ 課題
(1)ωx2とωy2の比が1:1のとき、どんなリサージュ図形になるか?
(2)ωx2とωy2の比が1:4または4:1のとき、どんなリサージュ図形になるか?
(注意)実験をするときは比例定数を変えた後、resetを押してからstartを押す。環境によっては角振動数を4にできないことがあります。
(3) (1),(2)のような運動になる理由を定量的に考察しなさい.
d2x/dt2 = - ωx2 x を解くと、x = ax sin(ωx t + δx)
同様に、y = ay sin(ωy t + δy)
これらに初期条件を与えて解く。
あとは角振動数の関係に注目。
投稿者 doraneco5675 : 14:04 | トラックバック
等速円運動と単振動
等速円運動(青)と単振動(赤)の比較をします。
また、角速度(回転・振動の速さ)を自由に変えることができます。
・等速円運動と単振動の関係を観察する。
・角速度を変化させたとき、等速円運動と単振動がどのように変化するのかを観察する。
□このアプレットからわかること
・単振動は等速円運動の正射影(円運動をしている物体に上から光を当てたときにできる影)に対応している。
・角速度は円運動の回転時間(周期)、単振動の振動時間(周期)に対応している。
□課題
上の観察結果を定量的に考察する。
投稿者 doraneco5675 : 13:48
放物線運動
放物線運動を観察します。初速度の打ち上げ角度を自由に変えることができます。
打ち上げ角度を変えたとき、運動がどのように変化するか。
□ このアプレットからわかること
初速度の打ち上げ角度を変えると放物運動の軌跡が垂直投げ上げ、斜方投射、水平投射に変えることができる。
別の見方をすれば、垂直投げ上げ、斜方投射、水平投射の違いは初速度の打ち上げ角度のみにあるということ。
□ 課題
上の観察結果を定量的に考察しなさい。
投稿者 doraneco5675 : 13:37
速度・加速度
速度・加速度を変えたときの運動の変化を観察します。
(1)加速度を0(m/s2)のままにして速度を変えると、物体がどのように運動するか。
(2)適当に速度を決めたあと加速度を変えると、物体がどのように運動するか。
□ このアプレットからわかること
自分なりに書いてみる。
□ 課題
速度・加速度と物体の運動の関係を定量的に考察する。
(ヒント)速度v = dx/dt ,加速度a = dv/dt = d2x/(dt)2
投稿者 doraneco5675 : 13:19
2004年12月02日
量の変化を表す(微積の準備)
目次
目的
観測によって得られる物理的意味を持った量を物理量と言います。
物理現象を解析するとき、物理量の変化を客観的に知りたいときがあります。
そこで、量の変化を表す方法である、変化量、平均変化率、比例と正比例を今から解説します。
変化量
ある量が変化したとき、量がどれだけ変化したかをあらわすものを変化量と呼びます。
ある量の変化量は、次のように定義します。
(●の変化量)=(●の変化後の量)-(●の変化前の量)
(●の変化量)=Δ●←Δはデルタと呼ぶ
と書くことにすれば、
Δ●=(●の変化後の量)-(●の変化前の量) -(*)←変化量の定義
となります。
この定義は日常生活でもよく使われています。
たとえば、
体重が50Kgから65Kgに太ったとき、
体重の変化量は、(*)より、
Δ(体重)=(体重の変化後の量)-(体重の変化前の量)
=(65Kg)-(50Kg)
=+15Kg
となるので、体重の変化量は+15Kgと求まります。
物理への応用として次の問題を解いてください。
物体がx軸上を動いている。 最初x = +100mの位置にいた物体が、x = -300m移動した。 移動後の位置はどこか?
<解答>
変化量の定義より、
Δ(位置)=(移動後の位置)-(移動前の位置)
⇔(-300m)=(移動後の位置)-(+100m)
⇔(移動後の位置)= -200m
平均変化率
「変化量」で体重の変化の例をあげました。
では、次のような体重の変化に違いはあるのでしょうか。
(1)1年で50Kgから65Kgになった。
(2)半年で50Kgから65Kgになった。
この二つは、どちらも体重の変化量は+15Kgですが、体重が変化した時間(時刻の変化量)が違います。
(1)では時刻の変化量は1年、(2)では時刻の変化量は半年です。
つまり、時刻の変化量に対して体重の変化量が違う、と言うことです。
((2)は半年で15Kg太ったのだから、(1)と同じ1年であれば30Kg太ることになりますよね)
この違いは、時刻の変化量が関係しているので体重の変化量だけでは表現できません。
そこで、2つの量の変化量が関係しているときの変化を表すものとして、平均変化率を定義します。
(▲に対する●の平均変化率)=(●の変化量)/(▲の変化量)
⇔(▲に対する●の平均変化率)=Δ●/Δ▲ -(**)
平均変化率の定義を使えば、
(時刻の変化量に対する体重の平均変化率)=(体重の変化量)/(時刻の変化量)
⇔(時刻の変化量に対する体重の平均変化率)=Δ(体重)/Δ(時刻)
となるので、
((1)の時間に対する体重の平均変化率)
=(+15Kg)/(1年)
=+15kg/年
((2)の時間に対する体重の平均変化率)
=(+15Kg)/(0.5年)
=+30kg/年
この結果から、同じ時間であれば(2)のほうが体重の変化が大きいことが分かる。
物理への応用として次の問題を解いてください。
(1)速度は、時刻の変化に対してどれだけ位置が変化したかを表したものである(速度の定義)。平均変化率の定義を使って速度を表せ。
(2)車が2時間で100Km走った。車の速度を求めよ。
(3)車が速度が60Km/時間(一定)で3時間走った。車の移動距離を求めよ。
<解答>
(1)速度は定義より、
(速度)=(位置の変化量)/(時刻の変化量)=Δ(位置)/Δ(時刻)
(2)速度の定義より、
(速度)
=Δ(位置)/Δ(時刻)
=(100Km)/(2時間)
=+50Km/時間
(注)今求めた速度は、2時間走ったときの平均の速度であって、2時間の常に+50Km/時間であるとは限らない。
(3)速度の定義より、
(速度)=Δ(位置)/Δ(時刻)
⇔(60Km/時間)=Δ(位置)/(3時間)
⇔Δ(位置)=(60Km/時間)×(3時間)=180Km
(注)平均変化率が一定でない、ここでは速度が一定でないとき、今解いたようにすぐに平均変化率の定義を使うことができない。
(2)、(3)の注については、物理のための微積で詳しく解説します。
時刻:時の一点
時間:ある時刻と別の時刻の時の間
つまり、⊿(時刻)= 時間
比例と反比例
2つの量の変化が関係しているときの変化の関係を表すものとして、比例と反比例があります。
・比例
ある量●がa倍になった時、別の量▲もa倍になることを、●は▲に比例すると言い、
●=k▲ (kは定数)
が成立する。
・反比例
ある量●がa倍になった時、別の量■が1/a倍になることを●は■に反比例すると言い、
●=k'/■ (k'は定数)
が成立する。
物理への応用として次の問題を解いてください。
ニュートンの第2法則によれば、質量mの物体に力Fを与えたときに生じる加速度aは力Fに比例し、質量mに反比例する。この関係を式で表せ。
<解答>比例・反比例の定義より、
加速度は力に比例する⇔a=k'F (k'は定数)
加速度は質量に反比例する⇔a=k"/m (k"は定数)
この二つを合わせて、
a=k F/m (kは定数)
↑
●が▲に比例し、■に反比例するとき、
●=k ▲/■ (kは定数)
が成立する。
(参考)
質量1Kgに加速度1m/s2を生じさせる力Fを1Nと定義すれば、
a=k F/m
⇔1 m/s2=k 1N/ 1Kg
⇔1=k ←(m/s2)=(N/Kg)
となり、比例定数kが1になるので、
a=k F/m ⇔ a=F/m ⇔ F=maを得る。
投稿者 doraneco5675 : 22:31
大学入試対策
基礎をある程度固めたら、どのレベルの大学を受ける人も過去問を解きましょう。
もちろんすぐに入試問題を解けるはずがありません。
型通りの基本問題と実戦の入試問題ではかなりギャップがあります(見かけ倒しなこともよくありますが)。
解けないのなら、解けるようになるまで問題集をやればいいじゃないかと思うかもしれません。
でも実際に入試問題を解くことによって、あなたの弱点、大学が求めているレベルが見えてきます。
これらを分析することで、明確な方針を立てることができます。
合格に必要なことがはっきりすれば、目的意識を持って復習、問題演習ができるので効果的です。
ここでは過去問の使い方とレベル別対策について紹介します。
中堅大学を受ける人
- 赤本などで過去問を実際に解いてみて苦手な分野を見つける
- 見つけた苦手の分野の問題を基本問題の演習のとき使った問題集で復習する
この2つをやれば十分です。
なぜなら中堅大学で合格点を取るのに必要なのは、
応用問題ではなく基本問題だからです。
一見難しい問題もありますが、大体は単に状況設定が複雑になっているだけなので赤本などの過去問の問題をたくさん解いていけば対応できるようになります。
過去問演習を得点力につなげるためには、
「わからない→答えを見よう」ではなくて「わからない→自分の知っている知識だけで解けるか考えよう」というように考え方をまるごと入れ替える必要があります。
私の場合、「問題が解けなかったときは、赤ペンで採点、解答の修正をし、青ペンでわからなかった原因、わかるようになるための対策をメモする」
ようにしていました。
このように自分で分析し記録すると、解けなかった原因が知識不足なのか、基本問題の理解不足なのかがはっきりするし、必要なときに素早く自分の弱点を復習できます。
必要以上のレベルの問題を解こうとして自爆はよくある失敗パターンなので、中堅大学を志望する受験生の人は注意してください。
短期間で難関大以上の合格を目指すのなら、基本は自分でやって、応用は予備校でやるという戦略は有効だと思います。しかし普通は予備校の授業の予習・復習で手一杯になるので、よほど強い意志がないと実行できません。
確実に中堅大学に合格したい人は、このようなリスクの高い戦略はやめましょう。
中堅大学を志望する人にとって応用レベルの問題は時間が余ったらやる程度のものですから。
難関大学以上を受ける人
中堅大学を受ける人に書いてある事と同じことをすれば合格最低点に近い点は取れます。
合格最低点+αを目指すには、さらに応用レベルの問題集の演習が必要です。
ここでは体系化のやり方別にアドバイスします。
□ 解法パターン重視
合格最低点+αを目指すなら一番短期間ですむやり方です。
問題集は「名問の森」、「理系標準問題集物理(名問の森よりやさしめ)」がうまくパターンがまとまっていて、典型的な入試問題が選ばれているのでお勧めです。
他の受験生に差をつけるためにはさらに難しい問題集(たとえば「難問題の系統とその解き方」)で大量に演習をする必要があります。
ただ、解法パターンのみに依存していて超難関大の問題で確実に高得点をとれるのかは疑問です。
□ 定義重視
普通の受験参考書は解法パターンに頼ってばかりでパズルを解いているみたいとストレスを感じている人や、受験物理ではなく物理学を学びたいと考えている人にお勧めのやり方です。
独学の場合、参考書に「新・物理入門」「要説物理学」を使い、問題集に「新・物理入門問題演習」、「SEGハイレベル物理」を使います。
ただ、定義重視の学習をした事のない人にとって「新・物理入門」は難しく感じるでしょう。また紹介した問題集は問題の解き方についての解説が薄いので、人によっては苦労した割に力がつかないこともありえます。
確実に身につけたいなら定義を重視して講義をしてくれる先生(有名なのは河合・東進の苑田先生)の講習を取ったほうがよいでしょう。
定義重視のやり方(本来の物理学のやり方)が身につけば、超難関大の問題で高得点・満点も夢ではありません。
※このやり方はいわゆる「微積物理」です。
□ 折衷型
解法パターンだけでは定義の部分がブラックボックスになっていて、問題を解くときにどの解法パターンを使うべきか迷ってしまうことがよくあります。
それをなくすために、よく迷ってしまう分野については「新・物理入門」のように定義重視の解説をしている参考書で調べて、ブラックボックスをなくすのが折衷型です。
問題集は解法パターン重視と同じ問題集を使います。解法パターン重視よりも時間は多めにかかりますが安定して点が取れるようになります。
このサイトでは、折衷型の人に役立つ物理の講義をしているので参考にしてください。
投稿者 doraneco5675 : 21:52
基本を身につける
物理の基本は、「図式化」「体系化」「基本問題の演習」に支えられています。
それぞれを簡単にまとめると次のようになります。
- 図式化:現象を図で的確に表す、概念・法則を具体的な図で理解する
- 体系化:現象と法則のつながりを理解し、自分なりの体系をつくる
- 基本問題の演習:入試レベルの問題を解くために最低限知っておかなくてはならない問題を演習する
図式化
図式化とは
図式化とはものごとを図でとらえることです。たとえば、道案内をするときに、地図を使うとわかりやすいですよね。
言葉で説明すると大変なことも、図を見せれば一発で分かることはよくあります。
図はたくさんの情報をシンプルな形で表すことができる便利なツールなのです。
物理にも図式化は役立ちます。
一般的に物理現象を考えるときには主に数式を使います。
一方、具体的な現象を考えるときには、状況を簡単に把握できる図が結構使えます。
今から、全ての人に役立つ現象の図式化と、初心者に有効な概念・法則の図式化を紹介します。
現象の図式化
現象の図式化とは、自分で具体的な現象の模式図を描くことです。
問題を解くとき、現象の図式化が役立ちます。
誰でも問題を解くとき、まずは問題文を見て具体的にどんな現象を表しているかを図で表しますよね。
図は現象を正しく理解していないと的確に描けません。
物理が得意な人ほど図をきちんと描いているし、物理が苦手な人ほど図を描かず(描けない?)式だけ立てて問題を解こうとします。
概念・法則の図式化
概念・法則の図式化とは、概念・法則を具体的な図で理解することです。
物理の概念・法則は、現象を数式、言葉でまとめたものです。
概念・法則は物理を体系的に理解するのには便利ですが、抽象的すぎて実感がわかないことがよくあります。
こういうときは概念・法則が表す具体的な図とセットにして考えてみると効果的です。
たとえば、速度・加速度の概念の違いはこのアプレットをみると実感がわいてくるのではないでしょうか。
実感がわくと抽象的にも考えられるようになります。
この方法は初心者の段階で特に有効ですので、積極的に使ってみてください。
図式化を身につける
普段心がけておくとよいことを紹介します。即効性はありませんが、やって損はありません。
□現象の図式化を身につける
・どんな問題でも現象を図で表す
・問題文中の言葉がどんな現象を表しているかを常に意識する
・どう描けば図で的確に現象を表すことができるかをまとめる
□概念・法則の図式化を身につける
・概念・法則を自分にとって実感がわく具体例とセットで理解する
・問題を解くときは、現象と概念・法則のつながりを意識する
参考書・講義を利用する際には、話し手(参考書の著者・講師)が書いた現象・概念・法則の図について、
・図の意味を理解できたか
・自分で図を再生できるか
・図を使って話し手と同じ説明ができるか
に注意しながら学習すると効果的です。
体系化
体系化とは
物理の世界は、バラバラに見える物理現象(具体)から法則(普遍)を導く(→帰納法)ことにより体系的にまとめられています。
そして、法則(普遍)から物理現象(具体)を導く(→演繹法)ことにより具体的な物理現象を解析することができます。
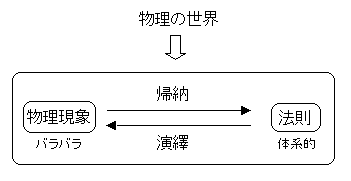
物理の体系化とは、物理現象と法則をつなげるもの、つまり物理現象を法則に帰納する過程と法則を物理現象に演繹する過程を理解し、使いこなせるようにすることです。
物理の体系を身につけると、どんな問題でも同じプロセスで解けるようになります。
物理が苦手な人は、現象と法則のつながりを無視(分かってない?)して単に覚えたことを、いきあたりばったりに当てはめて問題を解こうとします。
このやり方だといつまでたっても、解いたことのある問題しか解けません。
2つの体系化の方法
物理の体系化の方法は2つあります。
普通の参考書で使われているのは、解法パターンで体系化する方法です。この方法は深く理解しなくても問題が解ける長所があります。しかし、覚えることが多くなるし、パターンをうまく見抜けないと問題が解けません。
もう一つは定義から体系化する方法です。こちらは厳密に理解することが必要になるので大変ですが、一度分かってしまえば「パターンを見抜く」というパズルみたいなことをやる必要がなくなります。
体系化の例
体系化について知ってもらうために、具体的な例を2つ紹介します。
□解法パターンで体系化の例
→ドップラー効果の問題を分類して、法則の使い方を決める
ドップラー効果の公式を導き方は主に3つあります。
1.波源と観測者の距離を考えずに、波の式の持つ意味を利用して導く
2.波源と観測者の距離を考えて、波の式の持つ意味を利用して導く
3.波源と観測者の相対速度に注目した導き方
入試問題に対応するためには、すべての導き方を知っていなければなりません。
しかしこの3つの導き方にはそれぞれ長所と短所があります。
1の方法は、波の式(V = fλ)の図形的意味を理解していないと理解しにくい。
2の方法は、1の方法と同じように理解しにくい。しかし、「斜め方向のドップラー効果の問題」などの応用問題を解くのに使える。
3の方法は、応用問題には対応できない。しかし、ドップラー効果の公式をすぐに導ける(詳しくはドップラー効果の公式の簡単な作り方を参照)。
私が問題を解くときには、振動数、波長だけ求めればよい問題は3の方法を使い、「斜め方向の問題」などの応用問題であれば、2の方法を使うと決めていました。
人によっては公式をただ暗記している人もいるだろうし、2の方法だけで考えている人もいるでしょう。
これが問題を分類して、法則の使い方を決める、解法パターンでの体系化です。
□定義から体系化の例
→運動方程式から力学的エネルギー保存則、運動量保存則を導く
運動方程式、力学的エネルギー保存則、運動量保存則に次のつながりがある事を知っていますか?
力さえわかれば、運動方程式を解くことによってどんな運動でも解析できる。
しかし、必ずしも力を求めることができないので、力がわからなくても式を立てることができる力学的エネルギー保存則、運動量保存則に変形する。
このことを知っていれば「力学的エネルギー保存則を使うパターンの問題と見抜けなかったから解けなかった。」なんてことはなくなります。
なぜなら運動方程式の数式を見るだけで、それが解析的に解けるかどうか判断できるからです。
入試問題は必ず解があるので、運動方程式のままで解けない時点で力学的エネルギー保存則、運動量保存則のどちらかを使うとわかります(ちょっと解法パターン的な考え方ですが)。
これが定義に沿って具体的な問題を解く、定義での体系化です。
滑らかな曲がった斜面を下る物体
運動方程式:mr"= mg + N
束縛条件:斜面の情報
まっすぐな斜面の場合、斜面の傾きがわかれば垂直抗力は求まります。
しかし、この問題のように曲がった斜面では垂直抗力は簡単に求めることができません。そのため、入試問題でこの運動が出てきたら力学的エネルギー保存則を使うのだろうと推測できます。
曲がった斜面は力学的エネルギー保存則を使うのだとわざわざ覚える必要はないわけです。
自分なりの体系をつくる
普段から意識しておくと応用問題を解くときに違いが出ます。
・参考書、講義を参考にして、自分が使いやすい体系をつくる
・公式は導出過程を理解し、自分で導けるようにする
・どんな問題でも自分なりの体系に沿って解く
基本問題の演習
基本問題とは
基本問題は入試問題を解くために最低限知っておかなくてはならない問題です。
レベルとしては、教科書例題から入試標準ぐらいの問題です。
(問題のレベルについて詳しくは、受験校と必要な問題のレベルをどうぞ。)
演習の目的
・図式の方法、自分なりの体系への理解を深め、正しく使えるようにする
・誤って理解してしまったことを基本問題を通して修正する
・短時間で問題が解けるように、基本問題を論理の流れを含んで記憶する
基本問題はその場で考えるのではなく自然に手を動くぐらいの状態にしておかないと、入試問題を時間内に解くことができません。
ある程度できるようになると、試験は問題だけでなく時間との戦いでもあることに気づきます。
進め方のアドバイス
・丸暗記せず論理の流れを含んで記憶する
・理解し納得するだけでなく、必ず記憶する
・ひねった類題にも対応できるよう、図式の方法、自分なりの体系を整理する
十分に理解できていないときは、無理に覚えようとせず解説を読んですぐ次の問題に行くという方針でよいと思います。しかし、理解し納得しただけでは問題を解くのに使えないので、最終的には必ず自力で問題の解答を再現できるように記憶してください。
自力で問題を解けるようになったら、自分専用の解法マニュアルノートを作るのもおすすめです。
ノートを作ること自体が図式の方法、自分なりの体系の整理になります。
基本演習に適した問題集
高校物理の問題集には、 解法パターン(法則の使い方)を重視しているタイプ と 定義の厳密さを重視しているタイプ の二種類があります。
物理が苦手な人は、基本問題の演習をするときには必ず解法パターン重視の問題集を選んでください。
基本問題の演習の第一目標は自分なりに図式化、体系化できるようにすることです。
定義を厳密に理解することは大切です。しかし、知識量があまりない段階で厳密さにこだわっていると大量の時間がかかり効率が非常に悪くなります。そもそも初心者向けの定義重視の本が現時点ではありません。
不完全でもよいので、まずは核となる図の描き方、自分なりの体系を身につけることに力を入れてください。
不完全な部分は入試問題を解く力をつけるの段階で修正できるので心配いりません。
参考書について詳しくは、参考書の選び方を参照してください。
投稿者 doraneco5675 : 19:01
2004年12月01日
学習の姿勢
一番大切なのは、分からないことはできるだけ自分で調べ、考えることです。
これは大学受験だけでなく、大学に入ってからさらに大切になります。
分からないからといってすぐ人に聞いていてはダメです。
自分でいろいろ試行錯誤することが必要です。
まずは分かっていること、分からないことを自分で整理しましょう。
そうすると自然に「なぜ?」と具体的な疑問が出てきます。
出てきた疑問は参考書や講義を利用して自分で調べ解決しましょう。
調べてもどうしても分からないときは、ネットの掲示板や先生に聞いてみるのも手です。それでも分からないときは、しばらくほおっておくのもよいでしょう。
分からないことが出てくるたびにこの作業を繰り返します。
すぐに答えを教えてもらうほうが効率的という意見もあります。たしかに知識量は手っ取り早く増えます。
しかしそういう知識は「分かった」ではなく「分かった気がする」状態のことが多く、応用することができません。
人に頼りっぱなしではなく、自分で調べ、考えるのが本当の学習であり、合格への近道なのです。
しかし、要領のいい勉強を提唱している和田秀樹氏さえも、最近の子供たちがあまりに勉強をしないため、基礎的な勉強をみっちりやれと主張を変えています。
分からないことがあったとき、自分で考えないと「なぜ?」と疑問は出てきません。
投稿者 doraneco5675 : 21:12