ホーム > 物理の講義 > 物理のための数学
 « 量の変化を表す（微積の準備） | 物理のための微積 | 物理のためのベクトル »

物理のための微積

目標

微積は物理を定量的（→現象を量で表す）に理解する道具です。

単純な現象のときは、量の変化も単純なので量の変化を表す（微積の準備）で紹介した変化量、平均変化率だけで処理できます。
しかし、複雑な現象になると、微積を使わないと正しく量の変化を表すことができません。

高校物理は、基本的に微積を必要としない、または回避できる範囲の現象を扱っています。

このため、物理を厳密に理解するためには微積が必要不可欠だと言えます。
しかし、微積に慣れていない普通の高校生にとって、微積をどうやって物理に使うのかよくわからないと思います｡

そこで、微積にあまり慣れていない人を対象に、物理の世界を理解するのに役立つ直観的な微積の考え方を解説します。
最後のほうで少し微積を使って物理の問題を解くための計算方法についても紹介します。

微積のポイント

微積の考え方の一番重要なポイントをまとめます。
微積の意味がわからない人にはピンと来ないかもしれませんがとりあえず頭に入れてください。

微積とは、微小区間（無限に細かい区間）で考えること。

微小区間は具体的な数字で表すことができないくらいの細かさです。これは私たちの常識を超えた細かさなので、次のような近似が可能になります。

微小区間では、
　・関数の「変数」を「定数」
　・図形の「曲線」を「直線」
と近似できる。

□関数の「変数」を「定数」と近似できるとは
ある変数が微小に変化したとき、他の変数の変化はほとんど0に近いので、他の変数の変化は無視して定数とみなそうということです。当たり前ですが、微小変化まで変化してないとみなしたら何も変化しないことになってしまい意味がなくなります。

□「曲線」を「直線」と近似できるとは
私たちが実感できる例があります。
地球は丸いですね。でも私たちにとって地面は平面に見えます。
これは私たちの見ることができる範囲が、地球の大きさに対してはるかに小さい（微小）からです。
つまり、どんな曲線でもすごく小さい範囲に限定すると直線とみなせるわけです。

これが微積の考え方のエッセンスです。
これから微分の考え方と積分の考え方について詳しく解説していきます。

[表１] 普通の世界と微小の世界の比較

	普通の世界	微小の世界
関数	変数	定数
図形	曲線	直線
	直接計算できない	直接計算できる

微分の考え方

微分とは、ある点での変化率、曲線の接線の傾き（直接計算できない）を
平均変化率、直線の傾き（直接計算できる）とみなすことです[表２]。

[表２] 微分の考え方

	普通の世界	微小の世界
関数	ある点での変化率	平均変化率
図形	曲線の接線の傾き	直線の傾き
	直接計算できない	直接計算できる

微分の考え方が物理に使われていることを、物理量：瞬間の速さを定義することを通して考えていきます｡

まず、中学生のときに学んだ速さの定義を確認しましょう。
速さの定義（中学生版）：
（時刻t から時刻t＋⊿t までの間の速さ）
＝（位置の変化量）／（時間の変化量）
文字式で書くと、v ＝ Δr／Δt　-(*)
となります。

量の変化を表す（微積の準備）の平均変化率でやりましたね。

位置の変化量と時間の変化量がわかれば、この定義式により時刻tから時刻t＋⊿tまでの間の速さを求めることができます。

では、瞬間の速さの定義もこの定義(*)を使えばよいのでしょうか？

ちょっと考えてみると、この定義式(*)を瞬間の速さの定義とするには無理があるのに気づきます。

たとえば、10ｋｍを2時間（時刻t から時刻t+2 の間）で走ったとしたら、
速さの定義式(*)により、速さ＝5Km／hと求まります。

しかし、2時間走っていて、全ての瞬間で速さが5Km／hとは限らないのではないでしょうか？
ある時刻では休んでいたり、また別の時刻では普段より速く走っているかもしれません。

つまり、(*)の速さの定義式は2時間走ったときの平均の速さを意味していて、走っている間のすべての瞬間の速さを表してはいないのです。

もしずっと同じ速さで走っていれば、（平均の速さ）＝（瞬間の速さ）になるけれど、一般的に成立することではないですよね。

一般的に言い直すと、(*)の速さの定義は時刻t から時刻t＋⊿t までの間の時間⊿tの平均の速さであり、時間⊿tの間の全ての時刻での瞬間の速さを表わしてはいない、ということです。

では、このとき瞬間の速さ、たとえば時刻t での瞬間の速さを定義するにはどうすればよいのでしょうか？

上の例で時刻tでの瞬間の速さを求める事ができなかったのは、
速さを測定する時間が⊿t＝2時間と長かったため、時刻tでの瞬間の速さから値のずれが大きくなってしまったためと考えられます。
逆に考えれば、速さを測定する時間を小さくすれば瞬間の速さからの値のずれが小さくなり、瞬間の速さに近づくのではないでしょうか。

そこで、瞬間の速さを、平均の速さの定義で測定時間⊿tを限りなく小さくにしたものと定義します。

式で書くと、
瞬間の速さの定義：
瞬間の速さv ＝ lim_Δt→0 Δr／Δt ＝ dr／dt　-(*')
となります。

「lim_Δt→0」はΔtを限りなく0（数値で表せないくらい小さい数）に近づけるという意味です。
Δ●→0のときΔ●はd●と表わします。このとき、●に依存する変化量Δ■もd■と表します。

これはある点での変化率は微小区間の平均変化率に一致するという微分の考え方です。

ここまでは瞬間の速さを関数的に考えてきました。
ここからは図形的意味を考えます。

まず準備として、平均の速さΔr／Δtの図形的意味を考えてみましょう。

rとtの関数が[図１]のようになっているとき、平均の速さ：Δr／Δtは点A（時刻t）と点B（時刻t＋Δt）を通る直線の傾きを表します。

先ほど説明したように、速さが時刻ごとに変わるとき直線の傾きは平均の速さを表しますが、瞬間の速さを表していません。

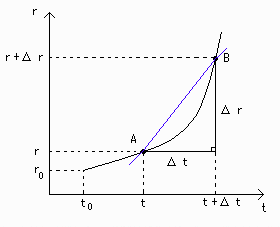
[図１] Δr／Δtの図形的意味

特に、速さが一定のときは、
v＝Δr／Δt (=一定)に(t₀,r₀)と(t,r)を代入して、
v＝(r-r₀)／(t-t₀)
⇒ r＝v(t-t₀) + r₀
となり、rとtの関数は直線になるので、
（rとtの関数の直線の傾き）＝（直線ABの傾き）＝（速さ）
となります。[図１']
（速さが一定のとき、Δｒ／Δｔは物理的意味を持つ）

速さが一定のとき、直線の傾きは平均の速さと同時に瞬間の速さを表す。
これは瞬間の速さを図形的に見るときの伏線になっています。

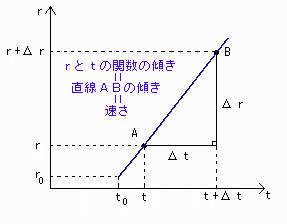
[図１'] 速さvが一定のときのΔr／Δtの図形的意味

ここから瞬間の速さの図形的意味を考えていきます。
瞬間の速さを求めるために測定時間Δtを0に近づけると、
[図２]のように点ＢはB0→B1→B2→・・・→Bn→・・・と点Aに近づいて行き、最終的に点Aと点Bはほとんど同じ点になります[図２]。

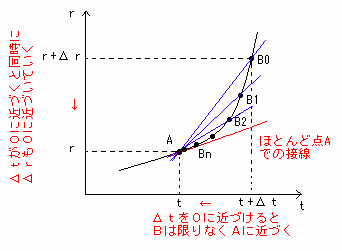
[図２] Δtを0に近づける

このとき、点Aの付近を見てみると、点Aと点Bの間隔が微小になっているため、
rとtの関数の曲線は点AB間で直線に近似でき直線ABと一致しています[図３]。
これは[図１']の状況と同じですよね。
ですから、このときの直線の傾きは瞬間の速さを表しています。

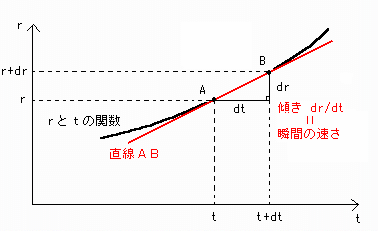
[図３] 点A付近の拡大図

[図３] は点A付近を非常に拡大して見ているので、点Aと点Bは離れているように見えます。
しかし、普通の世界では点Aと点Bはほとんど一致しているので、直線ABは点Aでの接線です。

以上より、瞬間の速さv ＝ lim_Δt→0 Δr／Δt ＝ dr／dt　-(*')の図形的意味は、
r-tグラフの接戦の傾きであると分かりました。

これはある点での接線の傾きは微小区間の直線の傾きに一致するという微分の考え方です。

Δとdの違い

Δ●とd●はどちらも●の変化量を表しています。

Δとdの違いは変化量の大きさにより決まります。

変化量が数値で表せるぐらい大きいときは、Δ●と書き、
変化量が数値で表せないくらい微小なときは、d●と書きます[図４]。

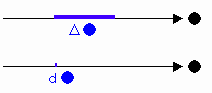
[図４] Δとdの違い

図形的には、Δが測定できる幅を持っているのに対して、
dは幅が測定できないくらい微小で私たちにとって点にしか見えない。

Δとｄの違いをふまえれば、
次の２つの運動方程式
m(d²r/(dt)²)＝F -(*) と m（Δ²r/(Δt)²)＝F -(**)
の違いが見えてきます。

(*)は、私たちには感じられないくらい微小な時間の変化の間（時刻tからt+dt）の運動方程式なので、ある瞬間(時刻t)の運動方程式とみなすことができます。

一方(**)は、時間の変化量がΔtなので、この式は瞬間ではなく一定の時間の間(時刻tからt+Δtの間)での運動方程式を平均したものと考えられます。[図５]

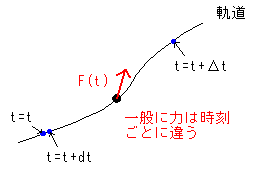
[図５] 運動方程式でのΔとdの違い

入試ではΔを微小量の変化とみなす場合もあります｡
d●は必ず微小量の変化を表します。
Δもdも「差」を表していますが、dは日常の概念を超えた「差」を表していることを意識しましょう。

積分の考え方

変数、曲線を無限個の微小な区間に分け、
変数に依存する変化量、曲線で囲まれた図形の面積・体積（直接計算できない）を、
変数に依存しない変化量、直線で囲まれた図形の面積・体積（直接計算できる）の集まり
としてとらえるのが積分です[表３]。

[表３] 積分の考え方

	普通の世界	微小の世界
関数	変数に依存する変化量	変数に依存しない（定数) の変化量の集まり
図形	曲線で囲まれた面積・体積	直線で囲まれた面積・体積の集まり
	直接計算できない	直接計算できる

積分の考え方が物理に使われていることを、物理量：移動距離を求めることを通して考えていきます｡

まずは、中学で習う方法で考えて見ます。
速さの定義（中学版）・平均の速さ(*)は
Δr ＝ vΔt　-(**)
と変形できます。

この式により、速さと時刻の変化量がわかれば移動距離を求めることができます。

たとえば、つねに時速5Km/hで2時間走ったとき、移動距離は(**)より10Kmと求めることができます。

しかし、この式には問題があります。
速さが時刻により変わるとき、どの時刻の速さを代入すればいいのでしょうか？

(**)は平均の速さの式を変形したものなので、ここに代入できるのは一定の速さ（平均の速さは一定）だけなのです。

もしずっと同じ速さで走っていれば、（平均の速さ）＝（瞬間の速さ）なので
移動中のどの瞬間の速さでも使えますが、一般的に成立することではありません。

では、一般的に移動距離（時刻tからt+Δtの間移動したとする）を求めるにはどうすればよいのでしょうか？

(**)の式を使って移動距離を求めることができないのは、時間が経過するとともに速さが一定ではなくなるためです。

この問題は、移動時間を無限小な時間に分け、微小な時間ごとに移動距離を求めることによって解決できます。

なぜなら、無限小な時間では速さは瞬間の速さとなり定数とみなせる（ある一瞬の速さだから値は変わらない）からです。
瞬間の速さは定数だから、平均の速さの式(**)から微小時間の間の移動距離を求める事ができます。
それを時刻tからt＋⊿t までたし合わせれば全体の移動距離になります。

たとえば、30分歩いたときの移動距離を求めるとき、移動時間30分の平均速度を使って計算するのではなくて､ 1秒ごとに速度を計測して1秒の間の移動距離を求めて、それを30分間分足し合わせるということです。

1秒の間に速度は変わるかもしれませんが、30分の平均速度を使うよりは、正確な移動距離が出そうですよね｡1秒よりもっと微小に分ければ、もっと正確な値が出てきます。

式で書くと、
速度が一定でないときも含む移動距離の定義：
微小時間dtの間の移動距離dr＝ vdt　（瞬間の速さの定義より）
時間⊿t の間の移動距離Δr ＝ ∫dr （区間：r(t₀)→r(t₀+⊿t)）＝ ∫vdt （区間：t₀→t₀+⊿t）　-(***)
となります。

「∫(インテグラル)」は微小変化を全て集めるという意味です。
数列でのΣに対応しています。

Δ●＝∫d● （区間：変化前の値→変化後の値）と表されます。
この式は、●の微小変化を集まれば●の変化量となることを意味しています。

これはある区間で変数に依存する変化量を、
区間を微小区間に分けて考えることにより、
変数に依存しない変化量の集まりとみなす
という積分の考え方です。

ここまでは移動距離を関数的に考えてきました。
ここからは図形的意味を考えます。

瞬間の速さのときはr-tグラフを書きましたが、移動距離ではv-tグラフを書きます。
vとtの関数は[図６]にあるように時刻とともに増加していくケースを考えます。

先ほど、Δr ＝ vΔt　-(**) は速度一定のときにしか使えないと解説しました。
このことを図形的に確認してみましょう。

(**)に点A(時刻t₀)のときの速さv₀を代入すると、
Δr ＝ v₀Δt となります。
これは[図６]の青色の四角形の斜線部分の面積ですが、速さが変わるときの移動量距離を表していないことは明らかです。

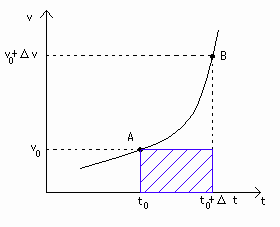[図６] vΔtの図形的意味

特に、速さが一定のときは、
移動距離Δr ＝ｖΔt (v=一定)
⇒ Δr ＝ vΔt（直線）となり、これは[図６']の斜線部分の面積（vとtの直線とt軸を含む四角形の面積）なるので、
（vとtの関数の直線とt軸を含む四角形の面積）＝（時間Δtの間の移動距離）-(☆☆)
となります。
（速さが一定のとき、ｖΔｔは物理的意味を持つ）

速さが一定のとき、vとtの直線とt軸で囲まれた面積が移動距離を表している。
これは移動距離を図形的に見るときの伏線になっています。

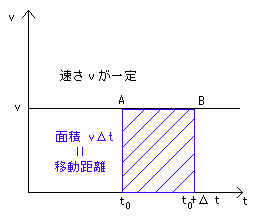
[図６'] 速さが一定のときのｖΔｔの図形的意味

ここから速度が一定でないときの移動距離の図形的意味を考えていきます。

移動距離を求めるとき、微小時間ごとに移動距離を求めます。
[図７]のように、微小時間dtを取ると、時刻tの付近ではvとｔの関数は斜めの直線に近似することができます。

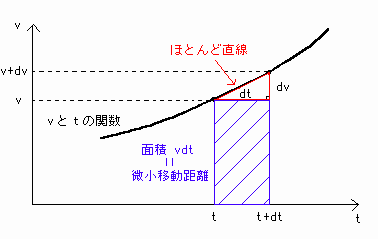
[図７] vdtの図形的意味

このとき、dr ＝ vdt　-(**')は、青色の四角形の面積を表します。

赤色の三角形の部分は無視していいのかと思った人もいるかもしれません。
実はdr ＝ vdtは青色の四角形の面積であり赤色の三角形を含んだ台形の面積でもあるのです。
日常感覚では理解できませんが、微小な世界では許される話なのです。

実際に、台形の面積を求めると、｛v＋（v＋dv）｝dt÷２＝vdt＋dvdt
でdvdtは微小な数同士の積なので0と近似してよく、結局台形の面積はvdtとなっています。

青色の四角形と赤色の三角形を含む台形の面積が等しいということは、
微小な面積を考えるとき、微小区間dtでvはほとんど一定とみなしてよいということです。
つまり、先ほどvとｔの関数は斜めの直線に近似と言いましたが、実際にはほとんど傾きが0の直線に近似されるのです。
これは[図６']の状況と同じなので、vdtの物理的意味は微小時間dtの間の移動距離といえます[図７]。

これより、時間⊿t の間の移動距離Δrの図形的意味が分かります。
定義より、
Δr ＝ ∫dr （区間：r(t₀)→r(t₀+⊿t)）
＝ ∫vdt （区間：t₀→t₀+⊿t）　-(***)
と表されます。
vdtは微小時間の移動距離であり、v-tグラフにおいて微小な四角形の面積を表しているので、
∫vdt （区間：t₀→t₀+⊿t）の図形的意味はvとtの関数とt軸で囲まれる部分の面積と分かりました[図８]。

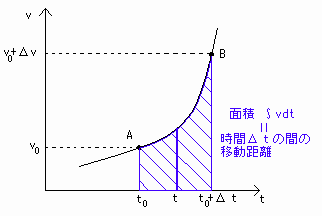
[図８] ∫vdtの図形的意味（区間：t₀→t₀+⊿t）

このように、微小区間に注目して、
まず微小変化量を求め、
それを足し合わせて全体の変化量を求めることを、
数学の言葉で積分といいます。

微積を使って物理を見る（初心者向け）

今までやってきたことをポイントにまとめます。
今までの話がよくわからなかった人もとりあえずここだけは押さえておきましょう。

＜Point＞微分の意味 ■＝d●／d▲は、次の二つの意味を持つ

ある▲に対する●の変化率を表す
●-▲グラフの接線の傾き

（例）v ＝dx／dt（■＝v（速度）、●＝x（位置）、▲＝t（時刻））のとき

あるtに対するxの変化率⇔ある瞬間のxの変化率⇔瞬間の速度
x-tグラフの接線の傾き

＜Point＞積分の意味 ■＝d●／d▲⇔微小変化：d●＝■d▲より、全体の変化：∫d●＝∫■ｄ▲（区間：●→●+⊿●、▲→▲+⊿▲)は、次の二つの意味を持つ

●の変化量（区間：●→●+⊿●)
■-▲グラフの面積（区間：▲→▲+⊿▲)

（例）∫dx ＝∫vdt （区間：x₀→x₀+⊿x、t₀→t₀+⊿t)　（■＝v（速度）、●＝x（位置）、▲＝t（時刻））のとき

位置の変化量（区間：x₀→x₀+⊿x)
v-tグラフの面積（区間：t₀→t₀+⊿t)

全体の変化：∫d●＝∫■ｄ▲（区間：●→●+⊿●、▲→▲+⊿▲)は、
微分の定義式：■＝d●／d▲から求まる微小変化：d●＝■d▲を足し合わせることによって求まる。

微積の計算を具体的にしない場合でも、上のポイントは知っておくと、
微積で表わされている式から、グラフの接線の傾きや面積がどんな物理的意味を持っているかが分かります。

たとえば、高校の教科書には電流の定義式：I ＝ΔQ／Δtとあります。
電荷Qは時刻によって変わる可能性があるので、一般的にはI ＝dQ／dtと微分を使って表さなくてはいけないことはもうわかりますよね。

上のポイントをふまえれば、微分の意味から、

ある瞬間の電気量Qの変化率
Q-tグラフの接線の傾き

ということが分かります。

また、I ＝dQ／dt ⇔ 微小変化：dQ ＝Idtより、
全体の変化：ΔQ ＝ ∫dQ＝∫Idt（区間が与えられているとする）が求まります。
この式は積分の意味から、

ある区間での電気量Qの変化量
ある区間でのI-tグラフの面積

ということが分かります。

参考として、微積を使って表されている式をいくつか紹介します。

・力学
　速度v ＝dr／dt
　加速度a ＝dv／dt
　仕事W ＝ ∫dW ＝ ∫F・dr
　仕事率dW／dt ＝ F・dr／dt
　運動量（力積）P ＝ ∫dp ＝ ∫Fdt

・熱力学
　気体がする仕事W_OUT＝ ∫dW_OUT ＝ ∫PdV

・電磁気
　電流I ＝ dQ／dt
　電位差V ＝ ∫dV ＝ ∫E・dr
　誘導起電力 V ＝－dΦ／dt

微積を使って問題を解く（上級者向け）

微積を使って力学の問題を解きます。
見慣れていないので複雑に見えると思いますが、高２で習うの微積と合成関数の微分を知っていれば理解できます。
数式を追うだけでなく、物理的意味を考えながら読んでみてください。

＜問題＞質量mの物体を滑らかな斜面をのぼる向きに初速v₀で動かした。

(1)物体の運動を求めよ。
(2)物体のエネルギー保存則を導け。

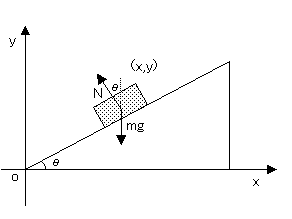
以下では、d●/dt=●'、d²●/dt²=●"と表す。
＜解答＞
(1)
図のように地面に平行な方向にx軸、垂直な方向にy軸を取る。

・運動方程式
　mx"(t)=-Nsinθ (1)
　my"(t)=Ncosθ-mg (2)
・初期条件
　x(0)=0,y(0)=0 (3)
　x'(0)=v₀cosθ,y'(0)=v₀sinθ (4)
・束縛条件
　tanθ=y(t)-y(0)/x(t)-x(0)（物体は常に斜面上にある） [t≠0]
　⇒y(t)=tanθx(t) (5) [t=0も含む]

目標：時刻tでの物体の位置(x(t),y(t))を求める。
(1)*cosθ+(2)*sinθよりNを消去：
mx"(t)cosθ+my"(t)sinθ=-mgsinθ
⇔x"(t)cosθ+y"(t)sinθ=-gsinθ (6)

(5)を２回時間微分する：
y"(t)=tanθx"(t) (7) ※d●/dt=●',d●'/dt=●"

(6),(7)よりy"(t)を消去：
x"(t)cosθ+tanθsinθx"(t)=-gsinθ
⇔x"(t)/cosθ = -gsinθ
∴x"(t)=-gsinθcosθ
また、(7)より、y"(t)=-g(sinθ)²

x"(t)=-gsinθcosθと初期条件(3),(4)より、
x'(t)=-gsinθcosθt+v₀cosθ
※∫d●=●+C(積分定数）、初期条件よりC=v₀cosθが決まる
x(t)=-(1/2)gsinθcosθt²+v₀cosθt
※∫●+C d●=(1/2)●²+C●+D(積分定数）、初期条件よりD=0が決まる

y"(t)=-g(sinθ)²と初期条件(3),(4)より、
y'(t)=-g(sinθ)²t+v₀sinθ
y(t)=-(1/2)g(sinθ)²t²+v₀sinθt

(2)
エネルギー保存則を求めます。

運動方程式の両辺に速度をかけると、
(1)*x'(t)+(2)*y'(t) ※仕事率dW/dt=F・V=Fx*Vx+Fy*Vy ：
mx"(t)x'(t) + my"(t)y'(t) =-Nsinθx'(t) +Ncosθy'(t) -mgy'(t)
⇔d/dt( (1/2)mx'(t)²+ (1/2)my'(t)² ) 　※d/dt(●²) = 2●●'
　 = N(-sinθx'(t) +cosθy'(t)) - mgy'(t)
さらに、(5)より-sinθx'(t) +cosθy'(t)=0 ,d/dt(y)=y'より、
⇔d/dt( (1/2)mx'(t)²+ (1/2)my'(t)² + mgy(t) ) = 0
この式は全ての時刻でエネルギーが一定であることをを表している。
つまり、エネルギー保存則を表す式である。

参考文献

図解雑学微分・積分、図解雑学わかる微分・積分
０から学ぶ入門書として最適
細野真宏の数IIIの微分積分が面白いほどわかる本（微分編）
微分の意味について Section1微分の定義に解説があります。
細野真宏の微分積分(原則編)・軌跡が面白いほどわかる本
積分の意味について、1.3.(1)体積の考え方（積分とは？）に解説があります。