ホーム > 物理の学習法
 « 学習の姿勢 | 基本を身につける | 大学入試対策 »

基本を身につける

物理の基本は、「図式化」「体系化」「基本問題の演習」に支えられています。
それぞれを簡単にまとめると次のようになります。

図式化：現象を図で的確に表す、概念・法則を具体的な図で理解する
体系化：現象と法則のつながりを理解し、自分なりの体系をつくる
基本問題の演習：入試レベルの問題を解くために最低限知っておかなくてはならない問題を演習する

今からこの３つを具体的に解説します。

図式化

図式化とは

図式化とはものごとを図でとらえることです。

たとえば、道案内をするときに､地図を使うとわかりやすいですよね。
言葉で説明すると大変なことも、図を見せれば一発で分かることはよくあります。
図はたくさんの情報をシンプルな形で表すことができる便利なツールなのです。

物理にも図式化は役立ちます。

一般的に物理現象を考えるときには主に数式を使います。
一方、具体的な現象を考えるときには、状況を簡単に把握できる図が結構使えます。

今から、全ての人に役立つ現象の図式化と、初心者に有効な概念・法則の図式化を紹介します。

現象の図式化

現象の図式化とは、自分で具体的な現象の模式図を描くことです。

問題を解くとき、現象の図式化が役立ちます。
誰でも問題を解くとき、まずは問題文を見て具体的にどんな現象を表しているかを図で表しますよね。
図は現象を正しく理解していないと的確に描けません。

物理が得意な人ほど図をきちんと描いているし、物理が苦手な人ほど図を描かず（描けない？）式だけ立てて問題を解こうとします。

問題に書かれている設定を図式化するとき、勝手に結果まで想像してはいけません。あくまで問題文に沿って現象を図で表すだけです。

概念・法則の図式化

概念・法則の図式化とは、概念・法則を具体的な図で理解することです。

物理の概念・法則は、現象を数式、言葉でまとめたものです。
概念・法則は物理を体系的に理解するのには便利ですが、抽象的すぎて実感がわかないことがよくあります。
こういうときは概念・法則が表す具体的な図とセットにして考えてみると効果的です。

たとえば、速度・加速度の概念の違いはこのアプレットをみると実感がわいてくるのではないでしょうか。
実感がわくと抽象的にも考えられるようになります。
この方法は初心者の段階で特に有効ですので、積極的に使ってみてください。

具体例に頼りすぎると、問題を解くときに自分の知っている具体例から勝手な想像をして混乱してしまうことがあります。理解が深まってきたら、必要に応じて言葉や数式で概念・法則を理解し直すようにしましょう。

図式化を身につける

普段心がけておくとよいことを紹介します。即効性はありませんが、やって損はありません。

□現象の図式化を身につける
　・どんな問題でも現象を図で表す
　・問題文中の言葉がどんな現象を表しているかを常に意識する
　・どう描けば図で的確に現象を表すことができるかをまとめる

□概念・法則の図式化を身につける
　・概念・法則を自分にとって実感がわく具体例とセットで理解する
　・問題を解くときは、現象と概念・法則のつながりを意識する

上に書いたことは全て自分でやるのは大変なので、必要に応じて自分が気に入った参考書・講義を利用しましょう。
参考書・講義を利用する際には､話し手（参考書の著者・講師）が書いた現象・概念・法則の図について、
　　・図の意味を理解できたか
　　・自分で図を再生できるか
　　・図を使って話し手と同じ説明ができるか
に注意しながら学習すると効果的です｡

体系化

体系化とは

物理の世界は、バラバラに見える物理現象（具体）から法則（普遍）を導く（→帰納法）ことにより体系的にまとめられています。
そして、法則（普遍）から物理現象（具体）を導く（→演繹法）ことにより具体的な物理現象を解析することができます。

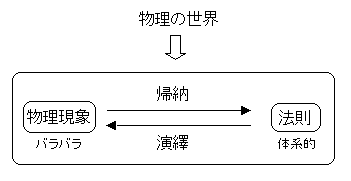
物理の体系化とは、物理現象と法則をつなげるもの、つまり物理現象を法則に帰納する過程と法則を物理現象に演繹する過程を理解し、使いこなせるようにすることです。

物理の体系を身につけると、どんな問題でも同じプロセスで解けるようになります。

物理が苦手な人は、現象と法則のつながりを無視(分かってない？)して単に覚えたことを、いきあたりばったりに当てはめて問題を解こうとします。
このやり方だといつまでたっても、解いたことのある問題しか解けません。

２つの体系化の方法

物理の体系化の方法は２つあります。
普通の参考書で使われているのは、解法パターンで体系化する方法です。この方法は深く理解しなくても問題が解ける長所があります。しかし、覚えることが多くなるし、パターンをうまく見抜けないと問題が解けません。
もう一つは定義から体系化する方法です。こちらは厳密に理解することが必要になるので大変ですが、一度分かってしまえば「パターンを見抜く」というパズルみたいなことをやる必要がなくなります。

解法パターンは、問題を分類して、解くために必要な法則の使い方の手順をまとめたものです。そのため解法パターンを使うときは、問題がどの分類に属するのかを見抜かなくてはなりません。

体系化の例

体系化について知ってもらうために、具体的な例を２つ紹介します。

□解法パターンで体系化の例
→ドップラー効果の問題を分類して、法則の使い方を決める

ドップラー効果の公式を導き方は主に３つあります。
　１．波源と観測者の距離を考えずに、波の式の持つ意味を利用して導く
　２．波源と観測者の距離を考えて、波の式の持つ意味を利用して導く
　３．波源と観測者の相対速度に注目した導き方
入試問題に対応するためには、すべての導き方を知っていなければなりません。
しかしこの３つの導き方にはそれぞれ長所と短所があります。

１の方法は、波の式（V = fλ）の図形的意味を理解していないと理解しにくい。
２の方法は、１の方法と同じように理解しにくい。しかし、「斜め方向のドップラー効果の問題」などの応用問題を解くのに使える。
３の方法は、応用問題には対応できない。しかし、ドップラー効果の公式をすぐに導ける（詳しくはドップラー効果の公式の簡単な作り方を参照）。

私が問題を解くときには、振動数、波長だけ求めればよい問題は３の方法を使い、「斜め方向の問題」などの応用問題であれば、２の方法を使うと決めていました。
人によっては公式をただ暗記している人もいるだろうし、２の方法だけで考えている人もいるでしょう。

これが問題を分類して、法則の使い方を決める、解法パターンでの体系化です。

□定義から体系化の例
→運動方程式から力学的エネルギー保存則、運動量保存則を導く

運動方程式、力学的エネルギー保存則、運動量保存則に次のつながりがある事を知っていますか？

力さえわかれば、運動方程式を解くことによってどんな運動でも解析できる。
しかし、必ずしも力を求めることができないので、力がわからなくても式を立てることができる力学的エネルギー保存則、運動量保存則に変形する。

このことを知っていれば「力学的エネルギー保存則を使うパターンの問題と見抜けなかったから解けなかった。」なんてことはなくなります。
なぜなら運動方程式の数式を見るだけで、それが解析的に解けるかどうか判断できるからです。

入試問題は必ず解があるので、運動方程式のままで解けない時点で力学的エネルギー保存則、運動量保存則のどちらかを使うとわかります（ちょっと解法パターン的な考え方ですが）。

これが定義に沿って具体的な問題を解く、定義での体系化です。

運動方程式のままで解けない例：
滑らかな曲がった斜面を下る物体
　運動方程式：mr"= mg + N
　束縛条件：斜面の情報

まっすぐな斜面の場合、斜面の傾きがわかれば垂直抗力は求まります。
しかし、この問題のように曲がった斜面では垂直抗力は簡単に求めることができません。そのため、入試問題でこの運動が出てきたら力学的エネルギー保存則を使うのだろうと推測できます。
曲がった斜面は力学的エネルギー保存則を使うのだとわざわざ覚える必要はないわけです。

自分なりの体系をつくる

普段から意識しておくと応用問題を解くときに違いが出ます。

　・参考書、講義を参考にして、自分が使いやすい体系をつくる
　・公式は導出過程を理解し、自分で導けるようにする
　・どんな問題でも自分なりの体系に沿って解く

自分なりの体系をつくり方には、解法パターン重視、定義重視、解法パターンと定義の折衷型があります。詳しくは入試対策で紹介します。

基本問題の演習

基本問題とは

基本問題は入試問題を解くために最低限知っておかなくてはならない問題です。
レベルとしては、教科書例題から入試標準ぐらいの問題です。
（問題のレベルについて詳しくは、受験校と必要な問題のレベルをどうぞ。）

演習の目的

　・図式の方法、自分なりの体系への理解を深め、正しく使えるようにする
　・誤って理解してしまったことを基本問題を通して修正する
　・短時間で問題が解けるように、基本問題を論理の流れを含んで記憶する

入試問題は基本問題がいくつか組み合わさってできています。
基本問題はその場で考えるのではなく自然に手を動くぐらいの状態にしておかないと、入試問題を時間内に解くことができません。
ある程度できるようになると、試験は問題だけでなく時間との戦いでもあることに気づきます。

進め方のアドバイス

　・丸暗記せず論理の流れを含んで記憶する
　・理解し納得するだけでなく、必ず記憶する
　・ひねった類題にも対応できるよう、図式の方法、自分なりの体系を整理する

ただ暗記するだけだと、すぐに忘れてしまうし、入試問題を解くのに使えません。まったく同じ問題が出るのなら話は別ですが。さっぱり分からないときは、その問題を飛ばすか、結果だけでも軽く覚えておくとよいでしょう。全体の理解が深まったとき、急に分かることはよくあります。

十分に理解できていないときは、無理に覚えようとせず解説を読んですぐ次の問題に行くという方針でよいと思います。しかし、理解し納得しただけでは問題を解くのに使えないので、最終的には必ず自力で問題の解答を再現できるように記憶してください。

自力で問題を解けるようになったら、自分専用の解法マニュアルノートを作るのもおすすめです。
ノートを作ること自体が図式の方法、自分なりの体系の整理になります。

基本演習に適した問題集

高校物理の問題集には､解法パターン（法則の使い方）を重視しているタイプと定義の厳密さを重視しているタイプの二種類があります。
物理が苦手な人は、基本問題の演習をするときには必ず解法パターン重視の問題集を選んでください｡

基本問題の演習の第一目標は自分なりに図式化、体系化できるようにすることです｡
定義を厳密に理解することは大切です。しかし、知識量があまりない段階で厳密さにこだわっていると大量の時間がかかり効率が非常に悪くなります。そもそも初心者向けの定義重視の本が現時点ではありません。

不完全でもよいので、まずは核となる図の描き方、自分なりの体系を身につけることに力を入れてください｡
不完全な部分は入試問題を解く力をつけるの段階で修正できるので心配いりません。

参考書について詳しくは、参考書の選び方を参照してください。

私の場合、最初から完璧にやろうとするより、最初は大まかにやって徐々に理解を深めるほうが効率的でした。