ホーム > 物理の学習法
« 大学入試対策 |
受験物理に微積は必要か?
| 微積が受験物理で役に立つ分野 »
受験物理に微積は必要か?
受験物理に微積は必要か?これは受験生が一度は考えたことがある問題です。この記事では、物理においてなぜ微積を使うのか?そして、受験生は微積を使うべきか?について考えていきます。
高校物理での微積の扱い
高校の物理の教科書では目に見える形で微積は使われていません。たとえば、厳密には速度は位置を時間tで微分したものと微分を使って定義します。
しかし、高校の物理の教科書には微積という言葉が使われず、瞬間の速度はΔr/Δtと定義されています(非常に短い時間Δtの間に物体が移動した量をΔrとしている)。
これは位置rを時間tで微分していると言っているのに等しいのですが、これが微分だとは高校の教科書には一言も書かれていません。
その結果として、この瞬間の速度の定義を平均の速度と同じものと勘違いしている高校生は多いのではないでしょうか。
他にも、微積を使わなければ厳密に説明できないことを、あいまいで天下り的に説明している部分がいくつかあります。
高校物理の教科書は、物理を厳密に記述するために必要な微積を使わずに、物理を体系化しているのです。それに従い多くの参考書では微積を使っていません。
「微積を使うべきかどうかの議論」の本当の論点
物理に微積を使うことは本質的には何を意味しているのかを考えていきます。高校物理で微積を使っている代表的な参考書である、駿台文庫「新・物理入門」の序文には次のことが書かれています。
高校生とりわけ受験生用に書かれた物理の参考書の大多数が、(中略)物理学の論理性と実証性を完全に無視し、天下りに書かれた「公式」なるもののバラバラな羅列を高々それらの当てはめのテクニックに終始している。
やみくもに丸暗記させられてきた「公式」なるものが、実は原理から論理的・数学的に導き出されるものであり、同時にまた、物理的現実をよく表す法則の一表現形式であることを納得したとき、初めてその面白さが分かる。
この序文に書かれている主張はまったく正しいと思います。これが微積を物理に使う意義だと私は思います。
わかりやすく言いなおすと、物理に微積をはじめとする数学を使うことは、定義を厳密にして物理を体系的に理解することなのです。
「微積を物理に使うべきかどうかの議論」の本当の論点は、「厳密な定義で物理を理解すべきかどうか」にあるのです。
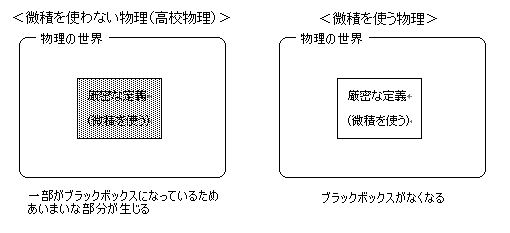
cf1. 受験生の間では微積物理という言葉が使われていますが、微積を使う物理とは別に独立して微積を使わない物理というものがあるわけではないです。[図1]にあるように厳密な定義の部分がブラックボックスになっているかどうかの違いだけで、他の部分については同じです。誤解している人がいるみたいなので注意してください。
[図1]微積を使う物理と使わない物理のイメージ

[図1]微積を使う物理と使わない物理のイメージ
cf2.「微積を物理に使うべきかどうかの議論」には、「微積を使うと問題が解きやすくなる」という論点もあります。この論点に興味がある人は微積が受験物理で役に立つ分野を参照してください。
受験物理と厳密な定義
受験物理において、厳密な定義を理解することが必要なのかについて考えていきます。まず私の考えを書きます。
厳密な定義を理解することが望ましい。しかし、受験の目標は限られた時間で合格に必要な問題を解けるようにすることなので、 時間対効果を考えた上で判断する必要がある。
考察するまでもないのですが、目標が物理の本質を理解することなら最初から微積を使って物理を理解することは有益です。しかし、受験本番までの時間は有限です。最初から厳密に理解しながら勉強するより短時間で効率的に得点力をつける方法があるのならそちらの方法をとるべきなのです。
以下では、この立場にたって受験生の学習段階別に考察をしていきます。
Case1 物理をまったく知らない~基礎固めをしている
このレベルの受験生は、現象・法則そのものを知らないので、どんな現象・法則があるのかを知る必要があります。
一般的に、知識がゼロに近い状態では抽象的な知識より具体的な知識のほうが理解しやすいことが知られています。
そのため、学習の初期段階では抽象的な厳密な定義を最初から学ぼうとするよりも、具体的な物理現象を通して現象・法則を理解していったほうが効率的だと考えられます。
Case2 入試対策をしている
このレベルになると、知らない現象・法則はほとんどなくなっているので、抽象的な厳密な定義を学ぶ準備はできているといえます。
しかし、準備ができているとしても、すべての受験生が微積を使って厳密な定義を学ぶべきかというと少し疑問があります。
それは次の疑問です。
・物理ができない原因は、微積を使っていないからだけなのか?
・普通の受験生が微積を使う物理に対応できるのか?
まずは、一つ目の疑問について考えてみます。
問題を解くときは、
・問われている現象を理解し、図で表す
・図で表した現象を式で表し、解く
という、ステップに分かれます。
微積が役立つのは図で表した現象を式で表し、解くというステップです。なぜなら、今までに書いてきたように法則の厳密な定義に微積などの数学が使われているからです。
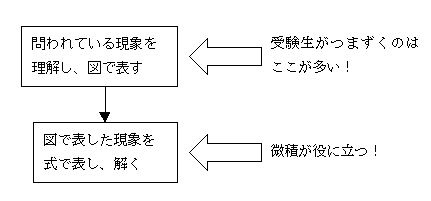
「ということは、やっぱり微積は必要じゃないか!」という声が聞こえてきそうですが、私の経験だと、受験生が入試問題を解けない原因は、最初のステップができていない、つまり微積の能力とは無関係な読解能力の不足であることが多いです[図2]。受験物理では、状況設定が複雑でなければ二つ目のステップで迷うことはありません。
[図2]問題を解くときの手順
だから、微積を使う前に、まずは現象を図式化できるようにする必要があります。
次に、二つ目の疑問について考えてみます。
高校生が物理を始めるのは基本的には2年生からで、この時点で微積を使いこなせる人は少ないし、さらに単に微積の計算ができるだけでは微積を使って物理現象を理解することはできない、という問題があります。
これを解決するには、独学で数学の問題を解くための微積の知識だけではなくて、物理現象を理解するのに役立つ微積の直観的な見方を身につけることが必要になります。
詳しく知りたい人は、物理のための微積を参考にしてください。
以上のことを考えると、基礎が身についた受験生であっても、下の二条件を満たしていない段階では、微積は使わないほうがよいと思います。
・現象を的確に図式化できる
・物理現象を理解するのに役立つ微積の直観的な見方ができる
cf. 物理の問題を解くときに微積を使う必要性を感じないのなら、微積を使う必要はありません。
「先生や友達が微積が必要だと言っている」とか、「微積を使うと頭がよさそう」という理由だけで使うのはどうかと個人的には思います。
もちろん、上に書いた理由がきっかけで微積を使いたいと思う人が多いと思います。しかし、厳密な定義に基づく物理はパターンを暗記する物理と違って能動的な学習が求められます。上に書いた理由だけでこのような学習が続けられるか疑問に思っています(特に独学の人は)。
「先生や友達が微積が必要だと言っている」とか、「微積を使うと頭がよさそう」という理由だけで使うのはどうかと個人的には思います。
もちろん、上に書いた理由がきっかけで微積を使いたいと思う人が多いと思います。しかし、厳密な定義に基づく物理はパターンを暗記する物理と違って能動的な学習が求められます。上に書いた理由だけでこのような学習が続けられるか疑問に思っています(特に独学の人は)。
まとめ
- 高校物理では微積は使われていない
- 物理に微積をはじめとする数学を使うことは、定義を厳密にして物理を体系的に理解すること
- 微積そのものが抽象的でやさしい概念ではないので、物理を苦手にしている段階で無理に微積を使う必要はない
- 現象を的確に図式化することができ、微積の直観的な見方を身につけたら、微積は物理のストーリーを理解する助けになるので必要に応じて取り入れるとよい
ホーム > 物理の学習法
« 大学入試対策 |
受験物理に微積は必要か?
| 微積が受験物理で役に立つ分野 »
投稿者 猫背の狸 、更新日 2006年12月30日