物理の学習法
学習の姿勢
一番大切なのは、分からないことはできるだけ自分で調べ、考えることです。
これは大学受験だけでなく、大学に入ってからさらに大切になります。
分からないからといってすぐ人に聞いていてはダメです。
自分でいろいろ試行錯誤することが必要です。
まずは分かっていること、分からないことを自分で整理しましょう。
そうすると自然に「なぜ?」と具体的な疑問が出てきます。
出てきた疑問は参考書や講義を利用して自分で調べ解決しましょう。
調べてもどうしても分からないときは、ネットの掲示板や先生に聞いてみるのも手です。それでも分からないときは、しばらくほおっておくのもよいでしょう。
分からないことが出てくるたびにこの作業を繰り返します。
すぐに答えを教えてもらうほうが効率的という意見もあります。たしかに知識量は手っ取り早く増えます。
しかしそういう知識は「分かった」ではなく「分かった気がする」状態のことが多く、応用することができません。
人に頼りっぱなしではなく、自分で調べ、考えるのが本当の学習であり、合格への近道なのです。
しかし、要領のいい勉強を提唱している和田秀樹氏さえも、最近の子供たちがあまりに勉強をしないため、基礎的な勉強をみっちりやれと主張を変えています。
分からないことがあったとき、自分で考えないと「なぜ?」と疑問は出てきません。
投稿者 猫背の狸 、更新日 2006年12月30日
基本を身につける
物理の基本は、「図式化」「体系化」「基本問題の演習」に支えられています。
それぞれを簡単にまとめると次のようになります。
- 図式化:現象を図で的確に表す、概念・法則を具体的な図で理解する
- 体系化:現象と法則のつながりを理解し、自分なりの体系をつくる
- 基本問題の演習:入試レベルの問題を解くために最低限知っておかなくてはならない問題を演習する
図式化
図式化とは
図式化とはものごとを図でとらえることです。たとえば、道案内をするときに、地図を使うとわかりやすいですよね。
言葉で説明すると大変なことも、図を見せれば一発で分かることはよくあります。
図はたくさんの情報をシンプルな形で表すことができる便利なツールなのです。
物理にも図式化は役立ちます。
一般的に物理現象を考えるときには主に数式を使います。
一方、具体的な現象を考えるときには、状況を簡単に把握できる図が結構使えます。
今から、全ての人に役立つ現象の図式化と、初心者に有効な概念・法則の図式化を紹介します。
現象の図式化
現象の図式化とは、自分で具体的な現象の模式図を描くことです。
問題を解くとき、現象の図式化が役立ちます。
誰でも問題を解くとき、まずは問題文を見て具体的にどんな現象を表しているかを図で表しますよね。
図は現象を正しく理解していないと的確に描けません。
物理が得意な人ほど図をきちんと描いているし、物理が苦手な人ほど図を描かず(描けない?)式だけ立てて問題を解こうとします。
概念・法則の図式化
概念・法則の図式化とは、概念・法則を具体的な図で理解することです。
物理の概念・法則は、現象を数式、言葉でまとめたものです。
概念・法則は物理を体系的に理解するのには便利ですが、抽象的すぎて実感がわかないことがよくあります。
こういうときは概念・法則が表す具体的な図とセットにして考えてみると効果的です。
たとえば、速度・加速度の概念の違いはこのアプレットをみると実感がわいてくるのではないでしょうか。
実感がわくと抽象的にも考えられるようになります。
この方法は初心者の段階で特に有効ですので、積極的に使ってみてください。
図式化を身につける
普段心がけておくとよいことを紹介します。即効性はありませんが、やって損はありません。
□現象の図式化を身につける
・どんな問題でも現象を図で表す
・問題文中の言葉がどんな現象を表しているかを常に意識する
・どう描けば図で的確に現象を表すことができるかをまとめる
□概念・法則の図式化を身につける
・概念・法則を自分にとって実感がわく具体例とセットで理解する
・問題を解くときは、現象と概念・法則のつながりを意識する
参考書・講義を利用する際には、話し手(参考書の著者・講師)が書いた現象・概念・法則の図について、
・図の意味を理解できたか
・自分で図を再生できるか
・図を使って話し手と同じ説明ができるか
に注意しながら学習すると効果的です。
体系化
体系化とは
物理の世界は、バラバラに見える物理現象(具体)から法則(普遍)を導く(→帰納法)ことにより体系的にまとめられています。
そして、法則(普遍)から物理現象(具体)を導く(→演繹法)ことにより具体的な物理現象を解析することができます。
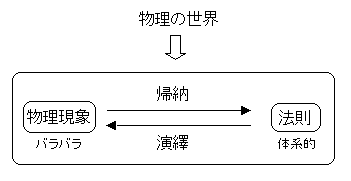
物理の体系化とは、物理現象と法則をつなげるもの、つまり物理現象を法則に帰納する過程と法則を物理現象に演繹する過程を理解し、使いこなせるようにすることです。
物理の体系を身につけると、どんな問題でも同じプロセスで解けるようになります。
物理が苦手な人は、現象と法則のつながりを無視(分かってない?)して単に覚えたことを、いきあたりばったりに当てはめて問題を解こうとします。
このやり方だといつまでたっても、解いたことのある問題しか解けません。
2つの体系化の方法
物理の体系化の方法は2つあります。
普通の参考書で使われているのは、解法パターンで体系化する方法です。この方法は深く理解しなくても問題が解ける長所があります。しかし、覚えることが多くなるし、パターンをうまく見抜けないと問題が解けません。
もう一つは定義から体系化する方法です。こちらは厳密に理解することが必要になるので大変ですが、一度分かってしまえば「パターンを見抜く」というパズルみたいなことをやる必要がなくなります。
体系化の例
体系化について知ってもらうために、具体的な例を2つ紹介します。
□解法パターンで体系化の例
→ドップラー効果の問題を分類して、法則の使い方を決める
ドップラー効果の公式を導き方は主に3つあります。
1.波源と観測者の距離を考えずに、波の式の持つ意味を利用して導く
2.波源と観測者の距離を考えて、波の式の持つ意味を利用して導く
3.波源と観測者の相対速度に注目した導き方
入試問題に対応するためには、すべての導き方を知っていなければなりません。
しかしこの3つの導き方にはそれぞれ長所と短所があります。
1の方法は、波の式(V = fλ)の図形的意味を理解していないと理解しにくい。
2の方法は、1の方法と同じように理解しにくい。しかし、「斜め方向のドップラー効果の問題」などの応用問題を解くのに使える。
3の方法は、応用問題には対応できない。しかし、ドップラー効果の公式をすぐに導ける(詳しくはドップラー効果の公式の簡単な作り方を参照)。
私が問題を解くときには、振動数、波長だけ求めればよい問題は3の方法を使い、「斜め方向の問題」などの応用問題であれば、2の方法を使うと決めていました。
人によっては公式をただ暗記している人もいるだろうし、2の方法だけで考えている人もいるでしょう。
これが問題を分類して、法則の使い方を決める、解法パターンでの体系化です。
□定義から体系化の例
→運動方程式から力学的エネルギー保存則、運動量保存則を導く
運動方程式、力学的エネルギー保存則、運動量保存則に次のつながりがある事を知っていますか?
力さえわかれば、運動方程式を解くことによってどんな運動でも解析できる。
しかし、必ずしも力を求めることができないので、力がわからなくても式を立てることができる力学的エネルギー保存則、運動量保存則に変形する。
このことを知っていれば「力学的エネルギー保存則を使うパターンの問題と見抜けなかったから解けなかった。」なんてことはなくなります。
なぜなら運動方程式の数式を見るだけで、それが解析的に解けるかどうか判断できるからです。
入試問題は必ず解があるので、運動方程式のままで解けない時点で力学的エネルギー保存則、運動量保存則のどちらかを使うとわかります(ちょっと解法パターン的な考え方ですが)。
これが定義に沿って具体的な問題を解く、定義での体系化です。
滑らかな曲がった斜面を下る物体
運動方程式:mr"= mg + N
束縛条件:斜面の情報
まっすぐな斜面の場合、斜面の傾きがわかれば垂直抗力は求まります。
しかし、この問題のように曲がった斜面では垂直抗力は簡単に求めることができません。そのため、入試問題でこの運動が出てきたら力学的エネルギー保存則を使うのだろうと推測できます。
曲がった斜面は力学的エネルギー保存則を使うのだとわざわざ覚える必要はないわけです。
自分なりの体系をつくる
普段から意識しておくと応用問題を解くときに違いが出ます。
・参考書、講義を参考にして、自分が使いやすい体系をつくる
・公式は導出過程を理解し、自分で導けるようにする
・どんな問題でも自分なりの体系に沿って解く
基本問題の演習
基本問題とは
基本問題は入試問題を解くために最低限知っておかなくてはならない問題です。
レベルとしては、教科書例題から入試標準ぐらいの問題です。
(問題のレベルについて詳しくは、受験校と必要な問題のレベルをどうぞ。)
演習の目的
・図式の方法、自分なりの体系への理解を深め、正しく使えるようにする
・誤って理解してしまったことを基本問題を通して修正する
・短時間で問題が解けるように、基本問題を論理の流れを含んで記憶する
基本問題はその場で考えるのではなく自然に手を動くぐらいの状態にしておかないと、入試問題を時間内に解くことができません。
ある程度できるようになると、試験は問題だけでなく時間との戦いでもあることに気づきます。
進め方のアドバイス
・丸暗記せず論理の流れを含んで記憶する
・理解し納得するだけでなく、必ず記憶する
・ひねった類題にも対応できるよう、図式の方法、自分なりの体系を整理する
十分に理解できていないときは、無理に覚えようとせず解説を読んですぐ次の問題に行くという方針でよいと思います。しかし、理解し納得しただけでは問題を解くのに使えないので、最終的には必ず自力で問題の解答を再現できるように記憶してください。
自力で問題を解けるようになったら、自分専用の解法マニュアルノートを作るのもおすすめです。
ノートを作ること自体が図式の方法、自分なりの体系の整理になります。
基本演習に適した問題集
高校物理の問題集には、 解法パターン(法則の使い方)を重視しているタイプ と 定義の厳密さを重視しているタイプ の二種類があります。
物理が苦手な人は、基本問題の演習をするときには必ず解法パターン重視の問題集を選んでください。
基本問題の演習の第一目標は自分なりに図式化、体系化できるようにすることです。
定義を厳密に理解することは大切です。しかし、知識量があまりない段階で厳密さにこだわっていると大量の時間がかかり効率が非常に悪くなります。そもそも初心者向けの定義重視の本が現時点ではありません。
不完全でもよいので、まずは核となる図の描き方、自分なりの体系を身につけることに力を入れてください。
不完全な部分は入試問題を解く力をつけるの段階で修正できるので心配いりません。
参考書について詳しくは、参考書の選び方を参照してください。
投稿者 猫背の狸 、更新日 2006年12月30日
大学入試対策
基礎をある程度固めたら、どのレベルの大学を受ける人も過去問を解きましょう。
もちろんすぐに入試問題を解けるはずがありません。
型通りの基本問題と実戦の入試問題ではかなりギャップがあります(見かけ倒しなこともよくありますが)。
解けないのなら、解けるようになるまで問題集をやればいいじゃないかと思うかもしれません。
でも実際に入試問題を解くことによって、あなたの弱点、大学が求めているレベルが見えてきます。
これらを分析することで、明確な方針を立てることができます。
合格に必要なことがはっきりすれば、目的意識を持って復習、問題演習ができるので効果的です。
ここでは過去問の使い方とレベル別対策について紹介します。
中堅大学を受ける人
- 赤本などで過去問を実際に解いてみて苦手な分野を見つける
- 見つけた苦手の分野の問題を基本問題の演習のとき使った問題集で復習する
この2つをやれば十分です。
なぜなら中堅大学で合格点を取るのに必要なのは、
応用問題ではなく基本問題だからです。
一見難しい問題もありますが、大体は単に状況設定が複雑になっているだけなので赤本などの過去問の問題をたくさん解いていけば対応できるようになります。
過去問演習を得点力につなげるためには、
「わからない→答えを見よう」ではなくて「わからない→自分の知っている知識だけで解けるか考えよう」というように考え方をまるごと入れ替える必要があります。
私の場合、「問題が解けなかったときは、赤ペンで採点、解答の修正をし、青ペンでわからなかった原因、わかるようになるための対策をメモする」
ようにしていました。
このように自分で分析し記録すると、解けなかった原因が知識不足なのか、基本問題の理解不足なのかがはっきりするし、必要なときに素早く自分の弱点を復習できます。
必要以上のレベルの問題を解こうとして自爆はよくある失敗パターンなので、中堅大学を志望する受験生の人は注意してください。
短期間で難関大以上の合格を目指すのなら、基本は自分でやって、応用は予備校でやるという戦略は有効だと思います。しかし普通は予備校の授業の予習・復習で手一杯になるので、よほど強い意志がないと実行できません。
確実に中堅大学に合格したい人は、このようなリスクの高い戦略はやめましょう。
中堅大学を志望する人にとって応用レベルの問題は時間が余ったらやる程度のものですから。
難関大学以上を受ける人
中堅大学を受ける人に書いてある事と同じことをすれば合格最低点に近い点は取れます。
合格最低点+αを目指すには、さらに応用レベルの問題集の演習が必要です。
ここでは体系化のやり方別にアドバイスします。
□ 解法パターン重視
合格最低点+αを目指すなら一番短期間ですむやり方です。
問題集は「名問の森」、「理系標準問題集物理(名問の森よりやさしめ)」がうまくパターンがまとまっていて、典型的な入試問題が選ばれているのでお勧めです。
他の受験生に差をつけるためにはさらに難しい問題集(たとえば「難問題の系統とその解き方」)で大量に演習をする必要があります。
ただ、解法パターンのみに依存していて超難関大の問題で確実に高得点をとれるのかは疑問です。
□ 定義重視
普通の受験参考書は解法パターンに頼ってばかりでパズルを解いているみたいとストレスを感じている人や、受験物理ではなく物理学を学びたいと考えている人にお勧めのやり方です。
独学の場合、参考書に「新・物理入門」「要説物理学」を使い、問題集に「新・物理入門問題演習」、「SEGハイレベル物理」を使います。
ただ、定義重視の学習をした事のない人にとって「新・物理入門」は難しく感じるでしょう。また紹介した問題集は問題の解き方についての解説が薄いので、人によっては苦労した割に力がつかないこともありえます。
確実に身につけたいなら定義を重視して講義をしてくれる先生(有名なのは河合・東進の苑田先生)の講習を取ったほうがよいでしょう。
定義重視のやり方(本来の物理学のやり方)が身につけば、超難関大の問題で高得点・満点も夢ではありません。
※このやり方はいわゆる「微積物理」です。
□ 折衷型
解法パターンだけでは定義の部分がブラックボックスになっていて、問題を解くときにどの解法パターンを使うべきか迷ってしまうことがよくあります。
それをなくすために、よく迷ってしまう分野については「新・物理入門」のように定義重視の解説をしている参考書で調べて、ブラックボックスをなくすのが折衷型です。
問題集は解法パターン重視と同じ問題集を使います。解法パターン重視よりも時間は多めにかかりますが安定して点が取れるようになります。
このサイトでは、折衷型の人に役立つ物理の講義をしているので参考にしてください。
投稿者 猫背の狸 、更新日 2006年12月30日
受験物理に微積は必要か?
この記事では、物理においてなぜ微積を使うのか?そして、受験生は微積を使うべきか?について考えていきます。
高校物理での微積の扱い
高校の物理の教科書では目に見える形で微積は使われていません。たとえば、厳密には速度は位置を時間tで微分したものと微分を使って定義します。
しかし、高校の物理の教科書には微積という言葉が使われず、瞬間の速度はΔr/Δtと定義されています(非常に短い時間Δtの間に物体が移動した量をΔrとしている)。
これは位置rを時間tで微分していると言っているのに等しいのですが、これが微分だとは高校の教科書には一言も書かれていません。
その結果として、この瞬間の速度の定義を平均の速度と同じものと勘違いしている高校生は多いのではないでしょうか。
他にも、微積を使わなければ厳密に説明できないことを、あいまいで天下り的に説明している部分がいくつかあります。
高校物理の教科書は、物理を厳密に記述するために必要な微積を使わずに、物理を体系化しているのです。それに従い多くの参考書では微積を使っていません。
「微積を使うべきかどうかの議論」の本当の論点
物理に微積を使うことは本質的には何を意味しているのかを考えていきます。高校物理で微積を使っている代表的な参考書である、駿台文庫「新・物理入門」の序文には次のことが書かれています。
高校生とりわけ受験生用に書かれた物理の参考書の大多数が、(中略)物理学の論理性と実証性を完全に無視し、天下りに書かれた「公式」なるもののバラバラな羅列を高々それらの当てはめのテクニックに終始している。
やみくもに丸暗記させられてきた「公式」なるものが、実は原理から論理的・数学的に導き出されるものであり、同時にまた、物理的現実をよく表す法則の一表現形式であることを納得したとき、初めてその面白さが分かる。
この序文に書かれている主張はまったく正しいと思います。これが微積を物理に使う意義だと私は思います。
わかりやすく言いなおすと、物理に微積をはじめとする数学を使うことは、定義を厳密にして物理を体系的に理解することなのです。
「微積を物理に使うべきかどうかの議論」の本当の論点は、「厳密な定義で物理を理解すべきかどうか」にあるのです。
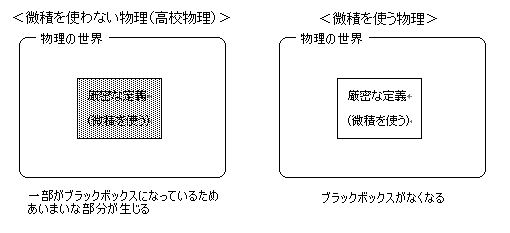
[図1]微積を使う物理と使わない物理のイメージ
受験物理と厳密な定義
受験物理において、厳密な定義を理解することが必要なのかについて考えていきます。まず私の考えを書きます。
厳密な定義を理解することが望ましい。しかし、受験の目標は限られた時間で合格に必要な問題を解けるようにすることなので、 時間対効果を考えた上で判断する必要がある。
考察するまでもないのですが、目標が物理の本質を理解することなら最初から微積を使って物理を理解することは有益です。しかし、受験本番までの時間は有限です。最初から厳密に理解しながら勉強するより短時間で効率的に得点力をつける方法があるのならそちらの方法をとるべきなのです。
以下では、この立場にたって受験生の学習段階別に考察をしていきます。
Case1 物理をまったく知らない~基礎固めをしている
このレベルの受験生は、現象・法則そのものを知らないので、どんな現象・法則があるのかを知る必要があります。
一般的に、知識がゼロに近い状態では抽象的な知識より具体的な知識のほうが理解しやすいことが知られています。
そのため、学習の初期段階では抽象的な厳密な定義を最初から学ぼうとするよりも、具体的な物理現象を通して現象・法則を理解していったほうが効率的だと考えられます。
Case2 入試対策をしている
このレベルになると、知らない現象・法則はほとんどなくなっているので、抽象的な厳密な定義を学ぶ準備はできているといえます。
しかし、準備ができているとしても、すべての受験生が微積を使って厳密な定義を学ぶべきかというと少し疑問があります。
それは次の疑問です。
・物理ができない原因は、微積を使っていないからだけなのか?
・普通の受験生が微積を使う物理に対応できるのか?
まずは、一つ目の疑問について考えてみます。
問題を解くときは、
・問われている現象を理解し、図で表す
・図で表した現象を式で表し、解く
という、ステップに分かれます。
微積が役立つのは図で表した現象を式で表し、解くというステップです。なぜなら、今までに書いてきたように法則の厳密な定義に微積などの数学が使われているからです。
「ということは、やっぱり微積は必要じゃないか!」という声が聞こえてきそうですが、私の経験だと、受験生が入試問題を解けない原因は、最初のステップができていない、つまり微積の能力とは無関係な読解能力の不足であることが多いです[図2]。受験物理では、状況設定が複雑でなければ二つ目のステップで迷うことはありません。
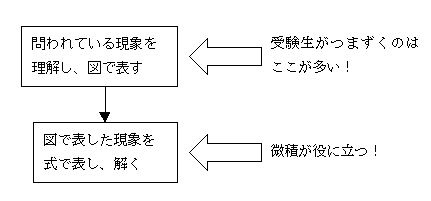
[図2]問題を解くときの手順
だから、微積を使う前に、まずは現象を図式化できるようにする必要があります。
次に、二つ目の疑問について考えてみます。
高校生が物理を始めるのは基本的には2年生からで、この時点で微積を使いこなせる人は少ないし、さらに単に微積の計算ができるだけでは微積を使って物理現象を理解することはできない、という問題があります。
これを解決するには、独学で数学の問題を解くための微積の知識だけではなくて、物理現象を理解するのに役立つ微積の直観的な見方を身につけることが必要になります。
詳しく知りたい人は、物理のための微積を参考にしてください。
以上のことを考えると、基礎が身についた受験生であっても、下の二条件を満たしていない段階では、微積は使わないほうがよいと思います。
・現象を的確に図式化できる
・物理現象を理解するのに役立つ微積の直観的な見方ができる
「先生や友達が微積が必要だと言っている」とか、「微積を使うと頭がよさそう」という理由だけで使うのはどうかと個人的には思います。
もちろん、上に書いた理由がきっかけで微積を使いたいと思う人が多いと思います。しかし、厳密な定義に基づく物理はパターンを暗記する物理と違って能動的な学習が求められます。上に書いた理由だけでこのような学習が続けられるか疑問に思っています(特に独学の人は)。
まとめ
- 高校物理では微積は使われていない
- 物理に微積をはじめとする数学を使うことは、定義を厳密にして物理を体系的に理解すること
- 微積そのものが抽象的でやさしい概念ではないので、物理を苦手にしている段階で無理に微積を使う必要はない
- 現象を的確に図式化することができ、微積の直観的な見方を身につけたら、微積は物理のストーリーを理解する助けになるので必要に応じて取り入れるとよい
投稿者 猫背の狸 、更新日 2006年12月30日
微積が受験物理で役に立つ分野
問題を解くときに微積が役に立つ分野
- 単振動
位置・速度・加速度・時間を求める
二体問題(ばねの両端におもりをつけて振動させる)を解く
- 交流回路
抵抗・コイル・コンデンサーの定義を知っていればリアクタンス・位相差などを覚える必要がなくなる
(詳しくは、微積を使う交流回路を見てください)
たとえば、単振動:mx" = -k x の一般解がx = a sinωt + b cosωtとなることを知っていれば、初期条件を与えることで、任意の時刻の位置、速度、加速度を求めることができます。
解法パターンで解く場合は、力学的エネルギー保存則を使うので、任意の時刻での位置、速度を求めることはできません。
微積を使えば解法パターンを覚えなくても、数学的な操作で必要な物理量を一般的に求めることができます。
意欲がある人は微積を使って解く方法を研究することをおすすめします。
物理量を定義する、公式を導くときに微積が役立つ分野
- 力学全般
位置・速度・加速度の定義と計算
運動方程式の定義と計算
仕事の原理を導く、エネルギー保存則を導く
運動量の原理を導く
- 熱力学全般
熱力学第1法則(エネルギー保存則)の計算
→仕事を求める、ポアソンの公式を導く
- 電気回路
電流、回路素子の電圧、エネルギーの定義
回路のエネルギー保存則を導く
電磁誘導による誘導起電力を求める
これらは微積を使ったからといって簡単に問題が解けるようになるわけではありません。
たとえば、等加速運動の問題を解くときに微積を使った場合のメリットは、高校教科書で与えられている等加速運動の公式を覚えていなくても導けることであって、運動方程式を立てる段階で力を正確に図示できていなかったら問題は解けません。
しかし、微積を使うことにより高校物理ではあいまいになっている物理量の意味や公式と公式のつながりをキチンと理解することができます。また、状況設定が複雑なときに正しく法則(たとえば、エネルギー保存則)を立てることができるメリットがあります。
微分積分を使わないと解けない入試問題は存在するか?
受験物理に微分積分は必要か?で書いたように、高校の教科書では微分積分を使っていることをはっきりと書いていません。そのため、入試問題は微分積分を使わなくても必ず解けるようになっているので、「微積を使わないと解けない問題があるのでは」という理由で微積を使う必要はありません。
<注>
一部の大学ではごくまれに、上に書いた物理量、法則が微積を使って定義され導かれていることを知っておかないと解けない問題が出題されることがあります。
たとえば、微積を使わないで問題を解くためには、⊿tが非常に短い時間であるとき、⊿sin(ωt) = ω cos(ωt) ・⊿tという近似式を与える必要がある問題で、この近似式が与えられていない問題が出題されたことがあるそうです。
これぐらいは数3をやった理系なら分かっとけってことなんでしょうね。
このような問題に対応するには、⊿を使って定義される物理量、法則は微分・積分につながっていることを知っておく必要があります。
詳しくは、物理のための微積を参考にして下さい(ここに書かれていることを知っていれば充分です)。
投稿者 猫背の狸 、更新日 2006年12月30日