« 2005年01月 | メイン | 2005年03月 »
2005年02月27日
0からはじめる磁気
目次
目標
まったく磁気を知らない人でもわかるレベルで、磁気について解説します。目標は、
- この記事を読んだ後で問題集の解答を自力で理解できるようになること
- 自分なりに磁気を視覚化・体系化できるようになること
磁気とはなにか?
磁石に他の磁石を近づけると、磁石は互いに引き合ったり反発したりします。
このような現象の根源となるものを磁気といいます。
磁気で働く力は、離れて(接触しないで)力が働く、引き合ったり反発したりする、という点で電気で働く力と類似しています。
電気の世界と対応させながら磁気の世界で何が力が生じる原因をつくるか、どんな力を受けるかについて説明していきます。
何が磁場をつくるか? ~電場との比較
クーロンの法則 ~静電気力と磁気力との比較
電気におけるクーロンの法則とは、
2つの電荷が静止しているとき、静電気力の大きさFは二つの電荷の間の距離rの2乗に逆比例し、それぞれの電気量q1および q2に比例する
(→F=K(q1q2/r2)というものです。
これに対応するものが磁気に存在していて、磁気でのクーロンの法則は、
磁石の間に働く力を磁極(磁荷)間の力に基づくとみなすと、磁極間の磁気力も静電気力の場合と同様に距離の2乗に逆比例し、それぞれの磁極の磁気量m1およびm2に比例する
(→F=K'(m1m2/r2)というものです。
このように磁気と電気は対応関係にあるので電気で使われた理論が磁気でも同じように使うことができます。
電気の世界では、力Fは電荷qと電場Eを用いて、
F = qE
と表されます。
また、電場の様子は電気力線を使って表されます。
磁気と電気は対応関係にあることをふまえれば、
磁気の世界では、力Fは磁荷mと磁場Hを用いて、
F = mH
と表されると推測できます。
このとき、磁場の様子は磁力線で表されます。
電荷q ⇔ 磁荷m
電場E ⇔ 磁場H
電気力線 ⇔ 磁力線
このような類推は確かに正しいのですがひとつ疑問点があります。
磁荷とはなんなのでしょうか?
電荷はこの世に存在するどんな物質にも含まれています。ガラス棒を絹布で摩擦すると物質は電荷を持つようになる、ということを習ったことがあると思います。
一方、磁荷を取り出す方法を習ったことがあるという人はいないでしょう。
実は、磁荷というものは存在しないからです。
磁石にはN極とS極が存在しています。これは、電荷で言えばプラスとマイナスの電荷に対応するものです。
もし、磁荷が存在しているなら、磁石を細かく切り刻むことにより、単独でN極とS極が表れるはずです。
しかし、磁石をどれだけ細かく切っても、切った端にN極とS極が表れ、単独でN極とS極を得ることはできません。
つまり、磁荷を見つけることができないのです。
では、磁荷が存在しないのなら、何が磁場をつくっているのでしょうか?
磁極はそういうものがあったほうが都合がよいという事情からできた概念であって現実には存在しません。そのため磁気力のクーロンの法則は、現象論的な法則とみなされています。
しかし、電磁気学の体系自身は磁極が単独で存在できる形になっているし、宇宙に単独の磁極が存在する可能性もないわけではありません。その意味では磁気力のクーロンの法則は、電気力の場合と同じ資格の基礎法則といえます。
何が磁場をつくるのか?
まず、次の問題を考えてください。
磁石を細かく切っていけば、つぎつぎと磁石を作ることができる。では、磁石を細かく切る回数に限界はあるか?
答えは、「切る回数に限界はある」です。
磁石を原子(陽子や電子)にまで細かく刻んでしまうと、これ以上は切ることができません。
一番小さい磁石は、原子なのです。
原子では、プラスの電気を持った陽子のまわりでマイナスの電気を持った電子が回転しています。
実は、この電子の回転が磁場をつくる正体なのです。
磁場は、磁荷がつくるのではなく、動いている電荷がつくるのです。
磁場のつくり方
繰り返しますが、動いている電荷が磁場をつくります。
つまり、
電荷が動く → 磁場が生じる
という因果関係が成立しています。
では、電荷が動くと磁場はどのようにつくられるのでしょうか?
磁場が生じる原因となる電荷の動かし方によって、磁場の生じ方は変わるので、電荷の動かし方で分類します。
(2つの現象に因果の関係があるとき、原因の部分を変えれば結果が変わるだろう、と考えるのは自然な考え方ですよね)
受験では、下の3つの電荷の動かし方しか出ないので覚えてください。
注意 以下では、電荷の集団が動くとき、つまり、電流を流したときに生じる磁場について考える。
電荷を直線に動かす(直線導線に電流 I [A]を流す)と、直線導線から半径r [m]離れたところに[図1]のように磁場 H(大きさ= I / 2πr)が生じる。
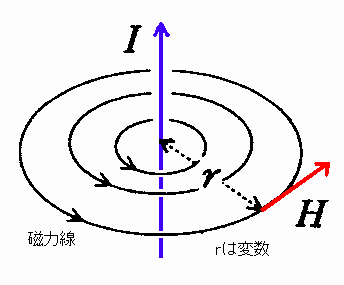
[図1] 電荷を直線に動かす(直線電流)
<Case 2> 電荷を円形に動かす(円形電流)
電荷を円形に動かす(円形導線に電流 I [A]を流す)と、半径r [m]の円形導線の中心で[図2]のように磁場H(大きさ= I / 2r)が生じる。
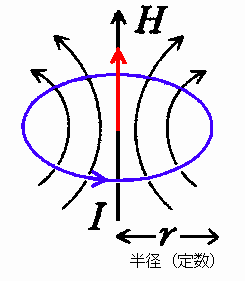
[図2] 電荷を円形に動かす(円形電流)
<Case 3> 電荷をソレノイドに沿ってに動かす
電荷をコイルに沿って動かす(ソレノイドに電流I [A]を流す)と、ソレノイドの中心で[図3]のように磁場H(大きさ= n I )が生じる。
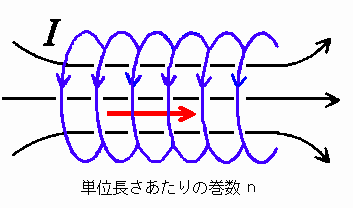
[図3] 電荷をソレノイドに沿ってに動かす
磁場の向きは、[図4]のように、右ねじを回す向きを磁場Hの向き、右ねじを回すと進む向きを電流Iの向き、と考えればどんな電荷の動かし方の場合でも求めることができます。
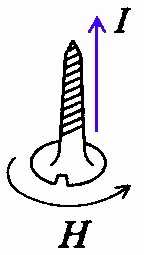
[図4] 右ねじの法則
磁束密度Bと磁場Hの関係
磁場の作用で物体が磁石になる現象を磁化といいます。
磁化に注目すると、磁束密度Bと磁場Hには下のような違いがあることがわかります。
- 磁束密度Bは磁化のしやすさを含む値
- 磁場Hは磁化のしやすさを含まない値
このとき、磁化のしやすさを表すものとして、透磁率μを使うと、
B=μH
という式が成立します。
磁場での現象は磁化のしやすさも関係するため、磁場Hではなく磁束密度Bで考える必要があります。
さらに詳しい話は、大学レベルの話になるのでここではふれません。
磁場から受ける力
電場では、電場に電荷を置くと電場から力を受けます。
磁場に電荷を置いても磁場から力を受けません。
では、どうすれば磁場から力を受けるのでしょうか?
その答えは次の実験結果からわかります。
磁石で作った磁場の中に電線を置き、電流を流さないときと電流を流したときの電線の様子を観察する。
<結果>
電流を流さないとき、電線に変化はなかった。
一方、電流を流したとき、電線が曲がった。[図5]
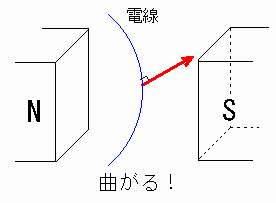
[図5] 磁場で電荷を動かす
この実験の結果から、磁場に電荷を置いただけでは磁場から力を受けないが、電荷を動かす(電流を流す)と磁場から力を受けるということがわかりました。
電荷の数で分類して、磁場から受ける力を2種類に分けます。
電荷 q [C]の荷電粒子を速度 v [m/s] で動かすと、[図6]のように速度vから磁場 Bの向きに右ねじを回したとき進む方向に大きさF=qvB の力を磁場から受ける。この力をローレンツ力という。 (ただし、速度 vと磁束密度 Bは直交)
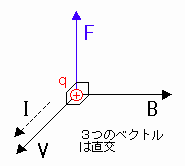
[図6] 荷電粒子が受ける力
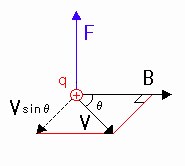
[図7-1] 速度の垂直成分をとる
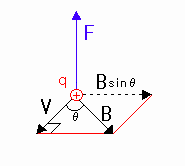
[図7-2] 磁束密度の垂直成分をとる
<Case 2 電流が流れる(荷電粒子の集団が動く)>
導線の長さが l[m]の導線に電流 I を流すと、[図6]のように電流I から磁束密度 Bの向きに右ねじを回した方向に大きさ F=IBlの力を磁場から受ける。この力を電磁力という。(ただし、電流 Iと磁束密度 Bは直交)
(注1)電流 I と磁束密度 Bが直交でないときは、電流 I の垂直成分は取れないので、[図7-2]のように磁束密度の垂直成分をとる。このとき、F=I(B sinθ)l
(注2)電磁力は導線内に存在する電子が受ける力の和なので、
(電磁力)=(導線内に存在する電子の総数)×(ローレンツ力)
が成立している。(この証明はできるようにする)
電磁誘導 ~磁場から電場をつくる
今から、電磁誘導という現象について考えていきます。まずは、準備として磁束密度、磁束線、磁束について説明します。磁束密度と磁束線の関係
磁束密度と磁束線を関係づけるために、次のように定義します。
定義:磁束密度と磁束線の関係
磁束密度 B のとき、1 m2あたりにB本の磁束線が面を垂直に貫くとする。[図8]
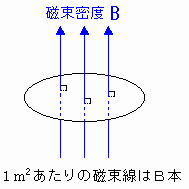
[図8] 磁束密度と磁束線の関係
磁束Φ(磁束線の総数)
ある領域S(面積Sm2)に存在する磁束線の総数を磁束Φ、とよぶ。
このとき、定義(磁束密度と磁束線の関係)より、
磁束Φ(磁束線の総数)=B×S
(ただし、磁束線と磁束線を貫く面は垂直(注))[図9]
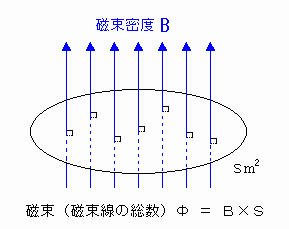
[図9] 磁束
(注)磁束線と磁束線を貫く面が垂直でないとき、定義のように磁束線と面が垂直になるように面の垂直成分[図10-1]または磁束密度の垂直成分[図10-2]を取る。
面の垂直成分を取る
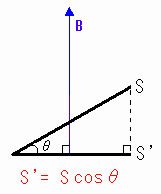
[図10-1] 面の垂直成分をとる
このとき、磁束Φ=B×S’=B×Scosθ
磁束密度の垂直成分をとる
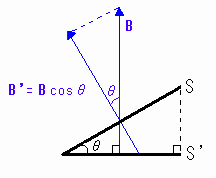
[図10-2] 磁束密度の垂直成分をとる
このとき、磁束Φ=B’×S=Bcosθ×S
当たり前ですが、どちらの垂直成分をとっても磁束Φの値は変わりません。
● 電磁誘導とはなにか?
「何が磁場をつくるのか?」で説明したように、
電荷を動かす → 磁場が生じる -(*)
という現象が起きるのならば、
逆の現象、つまり、
磁場を生じさせる → 電荷が動く -(**)
が起きるのではと考えられます。
実験により、確かに(**)が起きることが確認されました。
この現象を電磁誘導と呼びます。
さて、磁場を生じさせるとはどういうことでしょうか?
調べてみると、
磁場を生じさせる=磁束Φを時間に対して変化させる -(***)
ということがわかりました。
(**)と(***)をまとめて、電磁誘導とは、
磁束Φを時間に対して変化させる → 電荷が動く
ということと言えます。
電磁誘導の意味
電磁誘導とは、磁束を時間に対して変化させると電荷が動くという現象です。
では、電荷が動くと何が起こるのでしょうか。
そこで、磁束密度 Bの場所で導体棒を動かす場合を考えてみましょう。
[図11]のように導体棒を磁束密度 Bに対して垂直な方向に速度 vで動かす(Φ=BSのSの部分を時間に対して変化させる)と、[図12]のように電荷が動き陽子と電子がそれぞれ導体棒の端に移動する(陽子、電子の動く向きはローレンツ力で説明できる)。
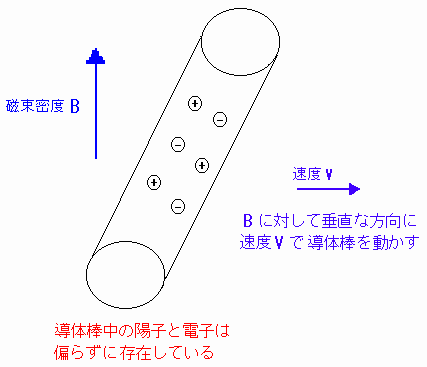
[図11] 導体棒を磁場で動かす
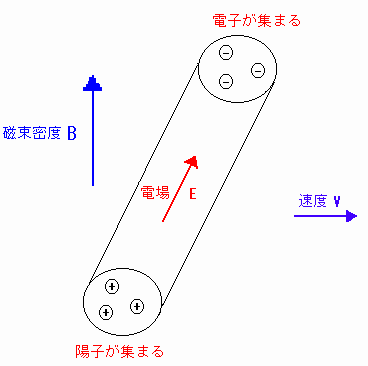
[図12] 磁場で導体棒を動かした後の状態
このとき、電荷が動くことにより、導体棒内で電場 Eが生じ、電位差が生じる。
電位差が生じているので、[図13]のように導体棒は電池化したと考えることができる。
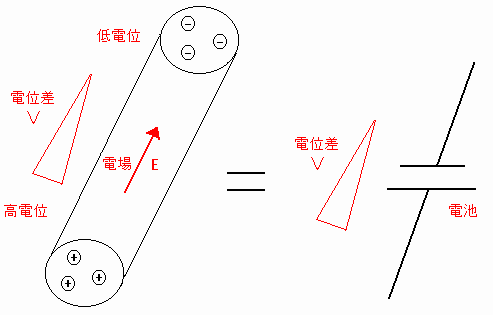
[図13] 導体棒の電池化
よって、電磁誘導とは導線(コイル)が電池化すること、といえる。
このとき生じる電位差Vを誘導起電力と言います。
<ローレンツ力による電磁誘導の解釈>
電子の電荷をe、導体棒の長さをlとする。
電子が受ける力は、磁場からの力と電磁誘導が起きたことにより生じた電場からの力を受けます。そして、電子は端で止まっているので、磁場からの力(ローレンツ力)と電場による力はつりあっていることがわかります。
よって、
(電場から受ける力の大きさ)=(磁場から受ける力の大きさ)
→e E =e v B
→E = v B -(*)
また、導体棒内では一様な電場が生じているので、
(電位差)=(電場の大きさ)×(導体棒の長さ)
→V = E l
が成立。
(*)を代入して、
誘導起電力 V = v B l
このとき、速度 vから磁束密度 Bの向きに右ねじを回したときにねじの進む向きが高電位となっています。
誘導起電力の求め方(ファラデーの法則)
一般にコイルの誘導起電力を求めるために、ファラデーの法則とレンツの法則を使います。
ファラデーの法則は、
誘導起電力 |V| = |ΔΦ/Δt|
であり、これから誘導起電力の大きさが求まります。
レンツの法則は、
磁束Φの変化を妨げる方向に誘導起電力は生じる(自然は変化を嫌う)、
というもので、これから誘導起電力の向きが求まります。
このふたつの法則を合わして、
誘導起電力 V = - ΔΦ/Δt (マイナスの符号がレンツの法則を表している(注))
と表して、これを普通はファラデーの法則とよびます。
ただし、微積を使わないで誘導起電力を求めるときは、誘導起電力の大きさと向きは別々に求めるので、誘導起電力の大きさを決めるのがファラデーの法則、向きを決めるのがレンツの法則と理解したほうが初心者の人にはよいと思います。
(注)マイナスの符号がレンツの法則を表す理由
コイルと同じ形の円形電流[図2]を見てください。
電流の流れる向きを右ネジをまわす向きとすると、右ネジの進む向きに磁場が生じています。このとき、右ネジが進む向きに回す方向の起電力を正とします。
レンツの法則によれば、磁束Φが増加するとき、右ネジが戻る向きに回す方向が高電位となる誘導起電力が生じます。これは、先ほど定義した起電力の向きとは逆なので、マイナスがつきます。
どうやって誘導起電力の向きが決まるかは、次の誘導起電力の向きが決まる仕組みを見てください
微積を使えば、誘導起電力 Vは、
V=-dΦ/dt
と表される。
微積を使えば誘導起電力の大きさと向きを別々に考える必要がなくなり機械的に解けるので、数学が得意な人は使ってみるのもいいかもしれません。
ただし、回路方程式の立て方(ループの向き、電流の向きの設定方法、回路方程式での電池・回路素子の符合の決め方)を分かっていないといけません。
最後に、誘導起電力の向きの決め方を確認します。
<誘導起電力の向きの決まる仕組み>
誘導起電力が起きる仕組みは次のようになっています。
レンツの法則より、
磁束Φが増加(減少)したとき、
磁束Φの増加(減少)を妨げるために(I)の向きに磁場B’が生じる。
(磁束Φ=BSなので、磁束の変化と逆向きに磁場B’をつくれば、磁束の変化と逆向きに別の磁束が生じ、磁束の変化を妨げることができる)
このとき、磁場B’を作るためには、(II)の向きに電流を流せばよく、(II)の向きに電流が流れているとき、コイルに(III)のような電池があると仮想できるので、誘導起電力は(III)のようになる。[図14]
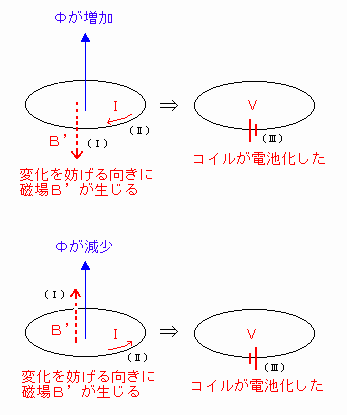
[図14] 誘導起電力の向き
投稿者 doraneco5675 : 16:56
2005年02月20日
リンク → 科学
物理
学習
物理の教室
Javaアプレットを用いた「動く物理」講座が特徴です。
本や授業では身につけにくい物理のイメージを養う事ができます。(相互)
楽習館
アニメや図を使って、現象、物理量、法則をわかりやすく解説しています。物理が苦手な人におすすめです。(相互)
PHYSICS is the WORLD.
物理現象のシミュレーションや数学の解説をしています。(相互)
分子のおもちゃ箱
物理シミュレーションのアプレット集です。分子の動きをビジュアル化することで、ミクロの世界を実感できます。(相互)
物理シミュレーションの部屋
Javaアプレットによる物理シミュレーション(主に高校範囲)を扱っています。(相互)
アインシュタインの相対性理論
相対性理論の初歩を分かり易く解説しています。なぜ運動する時計は遅れるのか。なぜ、運動する物体は縮むのか。光速度不変の謎にも迫ります。(相互)
【田原の物理】~たとえ話と微積分で物理が楽しくなる~
予備校講師による、物理の学習法、入試情報の紹介。(相互)
Wave Master 解波新書
波についての具体的な知識を凝縮したサイト(相互)
中川雅夫の大学受験物理講義「大学受験物理塾」
予備校での講義や参考書を補強する内容が中心です。
物理研究室
東京都立大学の物理科のページ。
高校と大学の物理・数学の解説をしています。
中川のビジュアル物理教室
高校レベルの物理がアニメや図解等で解説されています。また、大学入試情報もあります。
のりさんのパソコン物理
パソコンを使った自作の物理シミュレーション教材があります。物理現象のイメージをつかむのに役立ちます。
VERTUAL PHYSICS
物理現象がどのように起こるかを、JAVAを使って実験しています。物理現象のイメージをつかむのに役立ちます。
コミュニケーション
坂間勇ファンサイト
坂間先生ファンのためのサイトです。坂間先生の情報、掲示板、物理学講義などがあります。(相互)
Buturing
物理関係のウェブリング「ぶつりんぐ」。
理工系学生の集会所
高校生・大学生のための物理のページです。(相互)
AEUGホームページ
大学で学ぶ物理学における定義式などの物理関係、パソコン、環境問題について。また、東京理科大学に関する情報を公開しています。(相互)
IMAKOV's World
大学で学ぶ物理の各分野のまとめが紹介されています。(相互)
数学
学習
数学担当:ねえねえ水野さんのページ
数学参考書レビューの充実度はすごい。
高校数学の自習室
大学入試数学の重要典型問題を解説や数学質問掲示板があります。(相互)
baccyの受験数学総合研究所
数学参考書・問題集講評があります。
まなりんの高校数学の森
進路・学習についての相談、答案作成法など。(相互)
基礎からの高校数学
数学を苦手にしている人を対象に、基本からの勉強方法、参考書・問題集の使い方の提案をしています。(相互)
数学の質問・疑問掲示板
小・中・高・高専・大学の質問掲示板があります。メールマガジンも発行しています。(相互)
【難関大学突破の数学】Wiki
目指せ偏差値80/入試数学専門サイト【難関大学突破の数学】の読者のためのWiki(相互)
空がとっても青いから
自作テキストと、授業のHTML版が掲載されています。数学が苦手な人に参考になります。
高校数学の基本問題
教科書レベルの内容について詳しく解説されています。
数学の部屋
さまざまな数学の教材を提供しています。
場合の数・確率を勉強しよう!
タイトルどおりです。
恋する数学~好きになれば理解は早い~
数学のオリジナルチャートやセンター試験の過去問解説をピンポイントで提供してくれます!
化学
学習
Kyos Chem
化学の学習法、参考書紹介、センターに役立つWebテキスト、問題を解くときや知識を覚える時に使うWeb版テクニック、意見交換の掲示板などがあります。(相互)
CHEMBASE
有機・無機化学の問題・解説があります。丁寧でわかりやすい解説なので、化学に苦手意識がある人におすすめです。(相互)
Cherun's room
高校化学の解説と穴埋め問題があります。(相互)
恋する化学
化学の各項目を1枚のチャートにまとめた教材を販売。(相互)
楽しい高校化学
高校化学の解説をしています。
生物
学習
くりえいとPEN
生物の学習法や参考書の紹介など。
桐島浩樹の大学受験生物なんでも相談室
生物の質問を掲示板で答えてくれます。
理科総合
学習
理科総合ドットコム・【田原の理科総合】~予備校講師によるセンター対策法!~
理科総合の入試情報、学習法の紹介。
コンピュータ
学習
初級シスアド 初級システムアドミニストレーターへの道のり
学校・通信講座の選び方・学習方法・試験の取り組方の紹介。
Computer Scienceメジャーの会
アメリカでコンピューターサイエンスを勉強している日本人学生のためのHPです。
投稿者 doraneco5675 : 21:23
リンク → 受験
情報収集
受験生ネット=東大受験生集まれ!
東大受験生と東大生のための掲示板と一般掲示板があります。受験リンク集が充実しています。(相互)
18road
受験生の交流・方法交換の掲示板、勉強法・参考書の紹介があります。(相互)
GAKUSAN
学習参考書(英語)の紹介をメインテーマにしたホームページです。(相互)
We're alive
大学合格を目指す浪人・再受験生のためのページです。浪人・再受験生のための掲示板。合格体験記があります。(相互)
YOZEMI FRIENDS
代ゼミ生のための情報交換のためのHPです掲示板、チャット、代ゼミ講師ミシュラン、ランキングなどがあります。(相互)
よりみち
駿台生をはじめ受験生・大学生の学習・生活情報交換を目的としたページです。(相互)
宮の杜☆社会人よ大学へ行こう!!
社会人入試で大学受験しようとしている人たちのための交流WEBサイトです。(相互)
薬学生の部屋
薬学生・薬学関係者を対象に、国家試験・就職などの有益な情報の提供、知識の向上、情報交換を目的としたサイト。(相互)
学習支援
勉強法の部屋
銀さんのページです。自分に合った勉強法を確立するためのアドバイスが詳しく書かれています。(相互)
Twilight Mirage
医学部再受験生による勉強法の紹介。休止中です。(相互)
合格術を考える
勉強法と各科目の参考書の紹介。
For Me...
受験勉強および受験生応援、自分の英語勉強と趣味のことが中心のページです。(相互)
いいとこどりでいいじゃない
VVさんがおもしろいと思うことをいろいろ紹介しています。勉強法のコーナーもあります。(相互)
AK'S HOMEPAGE
AKさんによる参考書レビュー。(相互)
大学受験のために
大学受験のための参考書、予備校、塾についての意見。(相互)
Call Me KOMI!
予備校講師などでの受験指導の経験と知識を元に、英語を中心としたアドバイスがいろいろあります。掲示板、メルマガや受験相談なども。(相互)
大学受験生サポートサイト
地理関係を中心に、学習教材の選び方を解説しています。(相互)
高校中退から早稲田へ
高校を半年で中退した管理人の早大合格までの体験と学習方法を紹介。(相互)
受験勉強法BY現役京大生
管理人が昔、独学で受験勉強をしていたときの経験を元に、受験勉強について書いたサイト。(相互)
一発逆転☆大学合格術
偏差値40から早稲田に合格した現役早大生である管理人が、大学受験に関する様々なコツを紹介。(相互)
浪人、おめでとう!
浪人生で、理系、しかも国立をねらっているアナタに、役立ちます!(相互)
大学受験・全般・研究
大検から、二年で国立医学科に合格した、管理人の最強参考書戦術(相互)
京大生の受験術指南~受かる勉強法はこれだ~
現役京大生が自らの体験を踏まえて、勉強法や受験術を教えます。(相互)
受験勉強法Blog
元フリーター現役京大生による受験参考書勉強法。(相互)
これが合否を分ける!Z会と大学受験支援サイト
京大生と東大生が、Z会と大学受験情報、勉強法などを公開。(相互)
100日で偏差値20アップ!理系の大学受験勉強法
浪人後100日で偏差値20アップし京都大学入試に合格した、数学・英語・物理・化学の大学受験勉強法!(相互)
受験・入試・お勉強ステーション
受験を向かえる学生たちへの勉強法や入試に役立つ情報を提供しています。(相互)
勉強法Lab
効果的で結果の出る勉強法を教えます。(相互)
大学受験de東大受験~東京大学への道~
現役東京大学生が東大受験体験をもとに大学受験勉強法・おすすめの参考書を紹介。(相互)
ドラゴン桜を超える!大逆転の勉強法を紹介
大学受験生のための役立つ情報を、カテゴリー・教科別に紹介。(相互)
DONと来い★大学受験
大学受験を迎える高校生の強い味方!合格請負人がセンター試験の突破術を伝授します。(相互)
高校受験研究会、高校入試 偏差値の上がる中学生の勉強法
偏差値が伸びる中学生の勉強法を紹介しています。各教科の中学生用の教材レビューなど、コンテンツがとても充実しています。(相互)
最強の受験勉強法を考える
大阪大学出身、再受験経験者の管理人が「最も効率の良い勉強法とは」ということを追究するサイトです。(相互)
偏差値40台からの早稲田・慶応大学受験マニュアル
偏差値40台から、早稲田・慶応大を目指す受験生を応援します。(相互)
参考書データベース
参考書データベースでは、受験生が本当に使うべき参考書をレビューしています。(相互)
早稲田大学理工学部に合格する方法
早稲田大学理工学部の入学試験に合格する方法を実体験を基にご紹介します。他にも受験に役立つ情報を随時、提供していきます。(相互)
ロジカル大学受験術
大学受験に勝つための方法を紹介しています!!予備校に頼らず独学で効率よく勉強しましょう!!(相互)
受験生のサイト
現役高校生の大学受験ブログ
現役高校生が実行している大学受験のための勉強法を載せているサイト(相互)
受験情報
受験情報全般
見聞録.com
進学にともないひとり暮らしを始める受験生のための応援サイト。(相互)
受験生のための東京ひとり暮らしガイド
受験・入学を控えた学生に役立つ情報を提供。(相互)
大検・大学受験対策リンク集
大検・大学受験対策に役立つリンク集。(相互)
Dear受験生♪
大学受験や資格取得など
受験生のためのお役立ち情報リンク集。(相互)
リクルート進学ネット
大学ランキング
大学図鑑のお部屋
大学へのリンク
SCHOOL NAVI出版社
教学社Z-KAI(Z会)
SEG
中経出版
奨学金
日本育英会読売育英奨学会のご案内
朝日奨学会
産経新聞奨学会
毎日育英会
進学・留学のための奨学金情報
日本政府奨学金、地方自治体奨学金、外国政府奨学金、民間・公益団体奨学金など・・・ 奨学金を進学・留学に上手に利用して楽しい学生生活を送りましょう。(相互)
予備校・通信教育
河合塾・Kei-net
駿台予備学校
東進ハイスクール
Z-KAI(Z会)
Benesse Corporation
北辰館スクールのページ
千葉県松戸市にある小・中・高校生を対象にした文武両道の学習塾,北辰館スクールのホームページです。(相互)
大学受験・少人数制個別指導 東京学院
JR水道橋駅より徒歩1分の所にある大学受験の少人数制予備校。安価な学費で講義や個人指導が受けられる。創立64年目の老舗予備校。(相互)
Seminar Phenomenon Internet School
学習計画についてのアドバイス,数学・物理の質問掲示板,数学のゼミなどがある。(相互)
西早稲田教育研究所
研究者・専門家・教師による通信教育サイト。特に小論文指導を手厚く展開しています。(相互)
大阪TCC高等学院
大阪市都島区東野田町にある大阪TCC高等学院の紹介。大学受験科、大検科、ネットスクールがある。(相互)
株式会社アップのホームページ
関西に拠点を置き、地域と密着した教育体制が自慢。受験教育、学校授業準拠だけでなく、英会話、科学実験、パソコン教育を提供。(相互)
通信家庭教師の英学院
大学・大学院入試指導や大学・大学院補習を、大学教員や専門家が担当。学術論文の翻訳・校正や作成指導も行う。(相互)
BB-School
「大検」などの資格取得講座を映像学習できるインターネット通信講座サイト(相互)
インターネット家庭教師 ねっちゅう
ブロードバンドサービスの決定版!希望の「インターネット家庭教師ねっちゅう」指導で学力アップ!(相互)
プロ家庭教師 ポプラ工房
札幌で高校生から小学生までの理数科目を指導するプロの家庭教師(相互)
DC 大学入試指導センター
高校生を対象に”親身の指導”を心がけたアフターケアを展開(相互)
東京凰籃学院
難関大受験アドヴァイスは参考になります。
高卒認定(大検)
受験生のサイト
COSMOなページ
受験生の交流ページです。河合塾コスモ、高卒認定について紹介しています。(相互)
【高卒認定ナビ】(大検から高認へ)
高卒認定についての掲示板があり、高卒認定の情報集めに役に立ちます。(相互)
高校中退から早稲田へ
高校を半年で中退した管理人の早大合格までの体験と学習方法を紹介。(相互)
受験情報
高卒認定【高認】情報センター文部省
予備校
第一高等学院代ゼミバイパススクール
河合塾COSMOコース
駿台オープンスクール
TCC高等学院
高知市にあるTCC高等学院のサイトです。TCCの紹介、高卒認定の制度や勉強法についてのアドバイスがあります。
BB-School
「高卒認定」などの資格取得講座を映像学習できるインターネット通信講座サイト
大学生のサイト
のぶりんの部屋
小説、勉強、雑学などのぶりんさんの趣味を形にしたページです。(相互)
えいゆうの館
理学部生の えいゆうさんのページです。(相互)
Four Points
慎さんのページです。「大学生に50の質問」が興味深いです。(相互)
投稿者 doraneco5675 : 17:47
ドップラー効果の公式の簡単な作り方
ドップラー効果とは、波源または観測者が動くことにより、観測者の振動数が変わる現象です。
ドップラー効果の公式って皆さん知っていますよね。
こんなやつです。
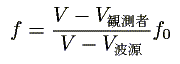
この公式をどのように導いていますか(または暗記していますか)?
実はこの公式は相対速度を知っていれば、簡単に導くことができます。
この記事ではその導き方を解説します。
準備として相対速度の定義を紹介します。
Aから見たBの相対速度は、
と定義される。
最初に、導き方をまとめます。
- 波源から見た波の式を立てる ((1)式とする)
- 観測者から見た波の式を立てる ((2)式とする)
- (2)÷(1)を実行 (これがドップラー効果の公式)
上のPointにしたがえば、簡単にドップラー効果の公式を導くことができます。
でも、「波源から見た波の式」「観測者から見た波の式」って何でしょう?
波の式は、
![]() ──── (☆)
──── (☆)
で定義されています。
参考書にはあまりふれられていませんが、波の式はいろんな視点(「地面」「波源」「観測者」)から見た波の式を考えることができます。
普段波の式として使っているものは、地面から見た(動いていない人から見た)波の式といえます。
ここで、視点別の波の式の立て方をまとめます。
- 速さvを視点から見た相対速さ(相対速度の大きさ)に変える
- (☆)の左辺が1.により変化したので、自動的に(☆)の右辺が変化する
- 波源から見たときと観測者から見たときの(☆)の右辺は変化の仕方は決まっているので、それに従い右辺を変形する
(このとき、波の式に現れる振動数fと波長λは、今考えている視点で観測される振動数fと波長λになる)
これから、視点別の波の式の右辺がどのように変化するか説明します。
一般的に考えるために波源も観測者も動いていると仮定します。
- 振動数f:
波源から見たときの波の式に使う振動数fは
波源の出す波の振動数fなので、波源が動いても動かなくても振動数fは変わらない - 波長λ:
数学的に見れば、波源が動くため左辺が変化していて、振動数fが変化しないので、波長λが変化することがわかる
(教科書を見れば、観測結果として波長λ変化することが載っているので参考にしてください)
- 波長λ:
観測者が動く事により波長λは変化しないため、観測者から見たときの波長λは波源から見たときの波長λと等しい
(たとえば、新幹線に乗って名古屋から東京へ行くとき、それによって名古屋と東京の距離が縮んだり伸びたりしませんよね。つまり、新幹線から見ても名古屋と東京の距離は変わらないわけです。) - 振動数f:
波源が動く事により波長λが変化し、観測者が動くことにより左辺が変化しているので、 観測者から見た振動数fは波源から見た振動数fと等しいとは限らない
最後に、確認として実際にドップラー効果の公式を導いて見ましょう。
速さをVの音を出す音源(波源)振動数f0が速さvで観測者に向かって動いている、観測者は音源に向かって速さuで動いているとしたとき、観測者に聞こえる音の振動数を求めよ。(ただし、音速V>v,u)
<解答>
<Point> 相対速度を使ったドップラー効果の公式の導き方
に従って、波源から見た波の式を求めます。(視点別の波の式の求め方の手順は<Point>視点別の波の式の立て方を参照してください)
問題文の音源(波源)が速さvで観測者に向かって動いているから、音の伝わる向きと音源の動く向きが同じことが分かります。
よって、音源から見た音波の速さは、音波の進む向きを正とすると、
|V-v|=|(+V)-(+v)|=V-v (音速V>v)
となるので、
音源から見た波の式は
V-v = f0 ×λ
となります(?)。
(とりあえず右辺の変化は考えず形式的に、地面から見た波の式の振動数f0と波長λをつかっています。もちろんこの式は正しくありません。)
地面から見たときの波の式(V = f0 ×λ)と違い波の式の左辺が変わったのだから、f0 または λのどちらかが変化しなければ、両辺のイコールの関係が成り立たなくなります。
そこで、<Point>波源から見たときの波の式(右辺の変化)をふまえれば、変わるのは波長λのほうだとわかります。
よって、変化したのが分かるようにλをλ’に置き換えて、音源から見た波の式を書き直すと、次のようになります。
V-v = f0 ×λ’・・・(1)
次に、観測者から見た波の式を求めましょう。
問題文の観測者は音源に向かって速さuで動いているから、音の伝わる向きと観測者の動いている向きは逆だと分かります。
よって、観測者から見た音波の速さは、音波の進む向きを正とすると、
|V-u|=|(+V)-(-u)|=V+u
となるので、
音源から見た波の式は
V+u = f0 ×λ
となります。
(とりあえず右辺の変化は考えず形式的に、地面から見た波の式の振動数f0と波長λをつかっています。もちろんこの式は正しくありません。)
<Point>観測者から見たときの波の式(右辺の変化)より、音源から見た波長と観測者から見た波長は変わらないので、音源から見た波の式の波長の部分にはλ’を代入します。また、振動数f0は変わる可能性があるので、fを代入します。
つまり、
V+u = f ×λ’・・・(2)
となります。
最後に、(2)÷(1)を計算すると、
V+u / V-v = f/f0 ⇒ f = (V+u / V-v) f0 ←答え
となり、求めたい観測者の振動数(ドップラー効果の公式の結果)を得ます。
やってることは一見ややこしいですが、慣れると簡単にドップラー効果の公式を導けるだけでなく、波長も簡単にもとまるので、ぜひマスターしてください。
(まとめ)
- 波源が動くと波長が変わる
- 波長はどこから見ても同じ長さ
投稿者 doraneco5675 : 15:55
要説物理学
コンセプトは新・物理入門と同じです。
解説は新・物理入門よりあっさりしていて、全体のつながりが見えやすくなっています。
数学によって物理はどのように体系化されているのかを手っ取り早く知りたいのならこちらをおすすめします。
とはいえ、普通の高校生が読み進めるのは大変なのですが。
投稿者 doraneco5675 : 12:35
新・物理入門
数学を積極的に使って物理を解説している有名な参考書です。
物理に数学を使うことによって、高校物理であいまいになっているところを厳密に理解できるようになります。
定量的な解き方で物理を極めたい人にとって最適な参考書と言えます。
問題演習用に新・物理入門問題演習があります。
普通の高校生が通読するのはつらいので、知りたいところだけを拾い読みする使い方もありです。
投稿者 doraneco5675 : 12:31
物理のための三角関数
物理で必要になる三角関数関係の公式をまとめました。
ここに出てくる公式、公式の導き方はすぐに使えるようにしましょう。
この程度は押さえていないと、参考書を読むのも大変だと思います。
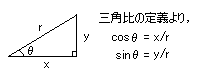
●三角比の定義と定理
[図1]のような角度θ[°]をとる直角三角形において、
sinθ= a/c
cosθ= b/c
tanθ= a/b
と定義する。
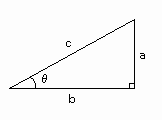
[図1] 三角比の定義
また、定義から次の二つの定理が成り立つ。
tanθ= sinθ/cosθ
(証明)
tanθ=a/b
=(a/c)/(b/c) ←分母分子をcで割った
=sinθ/cosθ←sin,cosの定義を代入した
sin2θ+cos2θ=1
(証明)
sin2θ+cos2θ
=(a/c)2+(b/c)2=(a2+b2)/c2
ここで、三平方の定理より、
a2+b2=c2が成立するので、
sin2θ+cos2θ=1
●余弦定理
[図2]のような三角形において、
a2=b2+c2-2bc cosθ
が成立する。
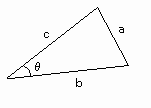
[図2] 余弦定理
●三角関数の定義と定理
[図3]のように半径1の円で(1,0)から逆時計回りに弧長θ[rad]をとったとき、
その円上の点のy座標をsinθ、x座標をcosθと定義する。
sinθ=y
cosθ=x
また、原点と点(x.y)を通る直線の傾きをtanθと定義する。
tanθ= y/x
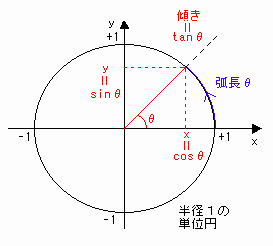
[図3] 三角関数の定義
三角比ではθは度(長さではない単位)を、三角関数ではθは弧長(長さ)を基準とした定義です。 物理ではθが変化する、つまりθを変数とする関数が必要になる場合が出てきます。 しかし、関数は長さを持つものでないと変数として使いにくいので、三角比を三角関数に拡張する必要があります。
<弧度法の定義>
[図4]において、弧長=半径×θ[rad](←弧度法の定義)なので、半径1の単位円では弧長=θ[rad]となります。
θ[rad]は、π[rad]=180[°]の対応関係が成り立つことから、θ[rad]/π[rad]=θ[°]/180[°]が成り立つことを使って求めています。
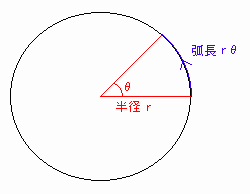
[図4] 弧度法の定義
<円のパラメータ表示>
三角関数の定義を、半径rの円に拡張すれば、
(x、y)=(r cosθ、r sinθ)
となります。
円のパラメータ表示は三角関数の定義を拡張したものなので、x座標sinをy座標cosとすることはできません。
また、定義から次の二つの定理が成り立つ。
tanθ= sinθ/cosθ
(証明)
tanθ=y/x←(0,0)と(x.y)を通る直線の傾き
=sinθ/cosθ←sin,cosの定義を代入した
sin2θ+cos2θ=1
(証明)
sin2θ+cos2θ
=x2+y2
ここで、(x,y)は半径1の単位円上の点なので、
x2+y2=1が成立する。
よって、
sin2θ+cos2θ=1
また、単位円を使えば、
sin(-θ)=-sinθ
cos(-θ)=cosθ
tan(-θ)=-tanθ
sin(π/2-θ)=cosθ
cos(π/2-θ)=sinθ
を得る。
これらの式は、単位円を使って左辺の値は+sinθ、-sinθ、+cosθ、-cosθのいずれに等しいかを考えれば求めることができる。
また、tanについては、tan=sin/cosから求めることができる。
●加法定理
sin(α+β)=sinαcosβ+cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
また、tan(α+β)=sin(α+β)/cos(α+β)より、
tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)
(証明)
tan(α+β)=sin(α+β)/cos(α+β)
=(sinαcosβ+cosαsinβ)/(cosαcosβ-sinαsinβ)
=((sinα/cosα)+(sinβ/cosβ))/(1-(sinαsinβ)/(cosαcosβ))←分母分子をcosαcosβで割った(tanが出てくる形にしたいから)
ここで、tan=sin/cosを使えば、
tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)となる。
また、
・β=-βとすれば、
sin(α-β),cos(α-β),tan(α-β)を得る。
・α=βとすれば、
二倍角の公式、半角の公式を得る。
・A=α+β、B=α-β⇒α=(A+B)/2、β=(A-B)/2とすれば、
和・差の変形公式を得る。
●合成公式
a sinθ + b cosθ =√(a2+b2) sin(θ+φ) (tanφ=b/a)
ただし、φは[図5]を満たすφである。
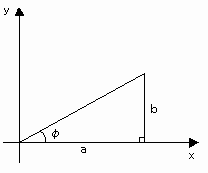
[図5] 合成公式
投稿者 doraneco5675 : 00:52
基本から学べる物理1B・2
駿台にしてはめずらしい初心者・中級者を意識した参考書です。
定量的な方法を身につけたいけど物理入門は難しいという人におすすめです。
初心者・中級者でも定性的な解説だとどうも納得できない所があれば、この参考書を見てみると良いでしょう。深いレベルのことまで詳しく書かれています。
投稿者 doraneco5675 : 00:21
2005年02月16日
物理のためのベクトル
目次
目標
ベクトルは物理の世界を理解するための道具として大切なものです。
しかし、物理の初心者は、数学としてはベクトルを知っているけれど、物理にベクトルを適用することができないことが多いのです(微積についても同じことが言えます)。これでは物理の体系を効率的に理解することができません。
そこで、この記事では数学にでるベクトルの問題を解くための解説ではなく、どうして、どうやって物理にベクトルを使うのかの解説をします。
ベクトルとは何か?
物理では、物理量(測定により得られる量)を表すために、数学の言葉で言う、スカラーとベクトルを使います。
ここでは、スカラーとベクトルの定義をし、ベクトルの表し方、スカラーとベクトルの違いについて説明します。
● スカラーとベクトルの定義
スカラーとベクトルは次のように定義されています。
- 大きさのみを表すものをスカラー
- 大きさ+向きを表すものをベクトル
● ベクトルの表し方
ベクトルは[図1]のように、
- 矢印の長さ=大きさ
- 矢印の先の向き=向き
として表される。
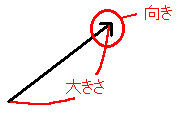
[図1]ベクトルの表し方
● スカラーとベクトルの違い
スカラーとベクトルの違いは、スカラーは向きを示すことができないのに対して、ベクトルは向きを示すことができることです。
この違いを理解していないと、物理量を正確に表すことができなくなります。
なぜベクトルを使うのか?
スカラーとベクトルの違いについては「ベクトルとは何か?」で紹介しました。
では、なぜベクトルを使わなくてはならない場合があるのでしょうか?
次の例題を考えてみてください。
- AとBの距離は5km
- Aから見てBは北東にある
このときスカラーで考えたとき、ベクトルで考えたとき、それぞれAから見てBはどこにあるかを図示しなさい。
<解答>
まず、条件が何を表しているかを考えます。
1は大きさ(距離)についての情報
2は向きについての情報
このことをふまえて、スカラーの場合、ベクトルの場合をそれぞれ考えて行きましょう。
スカラーで考える
スカラーは大きさのみを表すので、1の情報しか使うことができない。
1より、BはAを中心として半径5Kmの円上のどこかにある[図2]。
(2の情報が使えないのでこれ以上Bの位置はわからない)
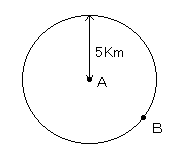
[図2]大きさの情報によるBの図示
このように、スカラーで考えると、Bの位置を完全に確定することができない。
→位置を表すのにスカラーは不適である!
ベクトルで考える
ベクトルは大きさ+向きを表すので、1と2の両方の情報を使うことができる。
まず1より、Aを中心とした半径5Kmの円上にBが位置していると考える事ができる[図2](ここはスカラーと同じ)。
次に2より、BはAからみて北東の向きにあることから[図3]の矢印上のどこかにBが位置していると考えることができる。
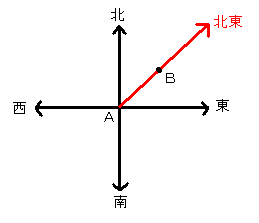
[図3]向きの情報によるBの図示
よって、[図2]と[図3]をあわせて考えれば、
Bは[図2]の円と[図3]の矢印の交点として求まる[図4]。
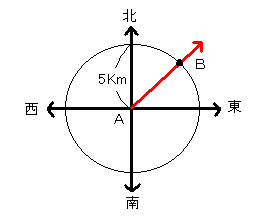
[図4]大きさ+向きの情報によるBの図示
このようにベクトルで考えるとBの位置を正確に定めることができるわけです。つまり、位置を表すのにベクトルは適しているのです。
例題の結果を考えれば、
位置を示すときにはベクトルを使わないと正確に示す事ができないということが分かります。
物理では位置を含めてベクトルを使わないと正確に示すことができない物理量がいくつか存在します(だから物理ではベクトルが必要になる)
(例)位置、速度、加速度、力、・・・
c.f.ベクトルを使わなくても、つまりスカラーで正確に示すことができる物理量もいくつか存在している。
(例)質量、時間、・・・
物理が苦手な人は、ベクトルとスカラーの区別をしていない人が多いので、問題を解くとき物理量はベクトルで表すのか、スカラーで表すのかを意識するようにしましょう。これが物理を得意科目にする第一歩です。
ベクトルの性質
ベクトルの性質について確認します(詳しくは、自分の使っている数学の参考書で確認してください)。
ベクトルは、大きさと向きを使いどの向きにどれだけ移動したかを表します。ベクトルを表示するためには矢印が使われます。
例えば、[図5]の点Aから点Bまでの移動量を![]() と書いてベクトルABと読み、出発する点Aを「始点」、到着する点Bを「終点」といいます。
と書いてベクトルABと読み、出発する点Aを「始点」、到着する点Bを「終点」といいます。
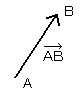
[図5]ベクトルAB
ベクトルは向きと大きさで決まる量なので、2つのベクトル
となるのは、[図6]のように、移動量が同じ、つまり、向きと大きさが同じときに限ります。すなわち、2つの矢印が平行移動で重なるとき、この2つのベクトルは等しいというのです。
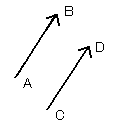
[図6]等しいベクトル
また、2つのベクトル
となるのは、[図7]のように、移動量が反対、つまり、向きが反対で大きさが同じときに限ります。すなわち、2つの矢印が平行移動で反対向きに重なるとき、この2つのベクトルの正負が逆になるのです。
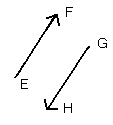
[図7]正負が逆のベクトル
さて、ここからはベクトルの合成、分解について説明します。
次の関係が成り立つのは明らかですよね[図8]。
(点Aから点Bまでの移動量)+(点Bから点Cまでの移動量)
=(点Aから点Cまでの移動量)
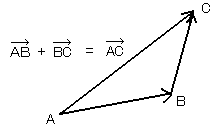
[図8]点Aから点Cへの移動
これをベクトルを使って書けば次のようになります。
![]() +
+![]() =
=![]() -(*)
-(*)
これをベクトルの合成といいます。
一方、(*)を逆から見ると
![]() =
=![]() +
+![]() -(**)
-(**)
これをベクトルの分解といいます。
このように、ベクトルでは、
2つ以上のベクトルを”つないで”1つのベクトルに合成
1つのベクトルを”わけて”2つ以上のベクトルに分解
することができるのです。
物理にベクトルを使うときに役に立つのは、1つのベクトルを”わけて”2つ以上のベクトルに分解できるという性質です。
この性質のおかげで、ベクトルを座標表示することができ、ベクトルを数式として処理する事ができるようになるのです。
ベクトルの座標化
ある点の位置はベクトルを使って[図9]のように図で表すことができます。
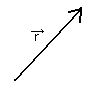
[図9]位置ベクトル
これを式で表すと
だから、図であるベクトルを数式化し計算を行いやすくするために、座標を導入する必要があるのです。
→座標は図形問題を計算問題に変換する働きをする
ベクトルの座標表示の方法をPointにします。
座標は必要に応じて自由に取り入れることができる -(*)
- 原点を決める(注)
- すべてのベクトルが{直線上、平面上、空間上}に存在するとき、
座標軸を{1本、2本、3本}導入する - ベクトルを座標軸上に分解する
- それぞれの軸について、
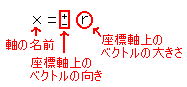 の型で表す
の型で表す
(注)位置ベクトルの始点は原点と一致させる。
上のPointをふまえて、[図9]の位置ベクトル(大きさはr)に座標を導入してみます。
位置ベクトルが直線上にあるとき、[図10]のようにベクトルと同じ向きを正として座標を導入すると、下のようにベクトルを数式化できる。
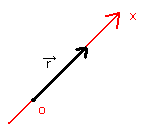
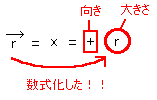
[図10]座標の導入例1
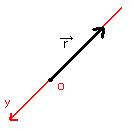
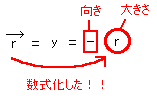
[図11]座標の導入例2
位置ベクトルが平面上にあるとき、[図12]のようにわざとθの角をなすように座標を導入すれば(座標は自由に取り入れる事ができる(普通は計算しやすいように座標を導入する))、下のようにベクトルを数式化できる。
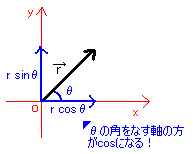
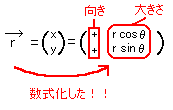
[図12]座標の導入例3
このように、ベクトルを座標表示すれば、ベクトルは数式化され物理の問題に適用しやすくなるのです。
物理が苦手な人は、ベクトルで表される物理量を扱っているときに、スカラーとベクトルの区別ができていない(ベクトルとわかっていない)ので、ベクトルの座標表示をすることができないのです。
そのために、放物運動、鉛直投げ上げ、鉛直投げ下げ、自由落下などの落体の運動を解くときに、お互いを関連づけることができずしかも公式として暗記してしまうのです。位置、速度、加速度がベクトルであることをわかっていれば、ベクトルの座標表示を使えば公式として暗記する必要が無くなることがわかるはずです。
落体の運動を公式として暗記している人は、等加速度直線運動の式
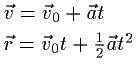
に座標表示した初速度、加速度を代入すれば、公式を暗記しなくても導ける事を確認してみてください。
まとめ
- 物理量はベクトル(大きさ+向き)かスカラー(大きさのみ)で表される
- ベクトルとスカラーの区別をしないと物理量は正確に表すことができない
- ベクトルは座標表示して数式化して計算する

 4点
4点
 5点
5点