ホーム > 物理の講義 > 波動
ドップラー効果の公式の簡単な作り方

ドップラー効果の公式の簡単な作り方

ドップラー効果とは、波源または観測者が動くことにより、観測者の振動数が変わる現象です。
ドップラー効果の公式って皆さん知っていますよね。
こんなやつです。
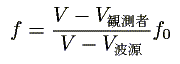
ドップラー効果の公式

この公式をどのように導いていますか（または暗記していますか）？


実はこの公式は相対速度を知っていれば、簡単に導くことができます。
この記事ではその導き方を解説します。


準備として相対速度の定義を紹介します。

＜相対速度の定義＞
Ａから見たＢの相対速度は、
相対速度の定義 ───― （★）
と定義される。


最初に、導き方をまとめます。

＜Point＞ 相対速度を使ったドップラー効果の公式の導き方
  1. 波源から見た波の式を立てる （(1)式とする）
  2. 観測者から見た波の式を立てる （(2)式とする）
  3. (2)÷(1)を実行 （これがドップラー効果の公式）

上のPointにしたがえば、簡単にドップラー効果の公式を導くことができます。

でも、「波源から見た波の式」「観測者から見た波の式」って何でしょう？

波の式は、
波の式 ──── （☆）

で定義されています。

参考書にはあまりふれられていませんが、波の式はいろんな視点（「地面」「波源」「観測者」）から見た波の式を考えることができます。

普段波の式として使っているものは、地面から見た（動いていない人から見た）波の式といえます。

ここで、視点別の波の式の立て方をまとめます。

＜Point＞ 視点別の波の式の立て方
  1. 速さｖを視点から見た相対速さ（相対速度の大きさ）に変える
  2. （☆）の左辺が1.により変化したので、自動的に（☆）の右辺が変化する
  3. 波源から見たときと観測者から見たときの（☆）の右辺は変化の仕方は決まっているので、それに従い右辺を変形する

    4. （このとき、波の式に現れる振動数fと波長λは、今考えている視点で観測される振動数fと波長λになる）


これから、視点別の波の式の右辺がどのように変化するか説明します。

一般的に考えるために波源も観測者も動いていると仮定します。

＜Point＞波源から見たときの波の式（右辺の変化）
  • 振動数f：
    波源から見たときの波の式に使う振動数fは
    波源の出す波の振動数fなので、波源が動いても動かなくても振動数fは変わらない
  • 波長λ：
    数学的に見れば、波源が動くため左辺が変化していて、振動数fが変化しないので、波長λが変化することがわかる
    （教科書を見れば、観測結果として波長λ変化することが載っているので参考にしてください）
（上の考察により、波源が動いていないなら振動数fも波長λも変化しない事がわかる）
＜Point＞観測者から見たときの波の式（右辺の変化）
  • 波長λ：
    観測者が動く事により波長λは変化しないため、観測者から見たときの波長λは波源から見たときの波長λと等しい
    （たとえば、新幹線に乗って名古屋から東京へ行くとき、それによって名古屋と東京の距離が縮んだり伸びたりしませんよね。つまり、新幹線から見ても名古屋と東京の距離は変わらないわけです。）
  • 振動数f：
    波源が動く事により波長λが変化し、観測者が動くことにより左辺が変化しているので、 観測者から見た振動数fは波源から見た振動数fと等しいとは限らない
（上の考察により、波源は動かず観測者のみが動く時でも、波源のみが動き観測者は動かない時でも、観測者から見た振動数fが変わることがわかる。）


最後に、確認として実際にドップラー効果の公式を導いて見ましょう。

＜問題＞
速さをVの音を出す音源（波源）振動数f0が速さvで観測者に向かって動いている、観測者は音源に向かって速さuで動いているとしたとき、観測者に聞こえる音の振動数を求めよ。（ただし、音速V>v,u)

＜解答＞
＜Point＞ 相対速度を使ったドップラー効果の公式の導き方
に従って、波源から見た波の式を求めます。（視点別の波の式の求め方の手順は＜Point＞視点別の波の式の立て方を参照してください）

問題文の音源（波源）が速さvで観測者に向かって動いているから、音の伝わる向きと音源の動く向きが同じことが分かります。
よって、音源から見た音波の速さは、音波の進む向きを正とすると、
|V-v|=|(+V)-(+v)|=V-v （音速V>v)
となるので、
音源から見た波の式は
V-v = f0 ×λ
となります（？）。
（とりあえず右辺の変化は考えず形式的に、地面から見た波の式の振動数f0と波長λをつかっています。もちろんこの式は正しくありません。）

地面から見たときの波の式（V = f0 ×λ）と違い波の式の左辺が変わったのだから、f0 または λのどちらかが変化しなければ、両辺のイコールの関係が成り立たなくなります。
そこで、＜Point＞波源から見たときの波の式（右辺の変化）をふまえれば、変わるのは波長λのほうだとわかります。
よって、変化したのが分かるようにλをλ’に置き換えて、音源から見た波の式を書き直すと、次のようになります。
V-v = f0 ×λ’・・・（１）

次に、観測者から見た波の式を求めましょう。
問題文の観測者は音源に向かって速さuで動いているから、音の伝わる向きと観測者の動いている向きは逆だと分かります。
よって、観測者から見た音波の速さは、音波の進む向きを正とすると、
|V-u|=|(+V)-(-u)|=V+u
となるので、
音源から見た波の式は
V+u = f0 ×λ
となります。
（とりあえず右辺の変化は考えず形式的に、地面から見た波の式の振動数f0と波長λをつかっています。もちろんこの式は正しくありません。）

＜Point＞観測者から見たときの波の式（右辺の変化）より、音源から見た波長と観測者から見た波長は変わらないので、音源から見た波の式の波長の部分にはλ’を代入します。また、振動数f0は変わる可能性があるので、fを代入します。
つまり、
V+u = f ×λ’・・・（２）
となります。

最後に、（２）÷（１）を計算すると、
V+u / V-v = f/f0 ⇒　f = (V+u / V-v) f0　←答え
となり、求めたい観測者の振動数（ドップラー効果の公式の結果）を得ます。


やってることは一見ややこしいですが、慣れると簡単にドップラー効果の公式を導けるだけでなく、波長も簡単にもとまるので、ぜひマスターしてください。

（まとめ）

  • 波源が動くと波長が変わる
  • 波長はどこから見ても同じ長さ

ホーム > 物理の講義 > 波動
ドップラー効果の公式の簡単な作り方

投稿者 猫背の狸 、更新日 2006年12月30日