« 2005年02月 | メイン | 2005年10月 »
2005年03月26日
橋元の理系物理IB・II頻出問題解法
橋元先生が標準レベルの入試頻出問題の解説をしています。解法の大原則で扱わなかった分野も扱っているので、橋元先生のやり方を好きな人なら、物理のエッセンスの代わりとして使うとよいでしょう。
ただし、物理のエッセンスやらくらくマスターと違い教科書レベルからやや易レベルの問題が少ないので別の問題集で補完する必要があります。学校で教科書レベルを終えているのなら、すぐにこの問題集をやり始めても問題はありません。
投稿者 doraneco5675 : 14:37
大学受験精選物理IB・II問題演習
(注)旧課程の参考書です
構成は、導入として各分野のポイントと解説の後、問題演習という構成になっています。
導入にある解説は深いレベルのことも書かれているので、自分なりの体系を深めるのに役立ちます。
問題は入試標準レベルが中心で、問題数は多すぎず少なすぎず使いやすいです。
投稿者 doraneco5675 : 14:26
漆原晃の物理 物理I・II明快解法講座
現象、法則、解法パターンの説明と重要問題の演習という構成になっています。全体の雰囲気は橋元先生に近く、クセのない橋元式といった感じです。エッセンスのように問題数が多く、説明が硬い本ではやりにくいと感じている人におすすめです。
ただし、この本は問題数が少ないので、他の本や過去問で問題演習をきちんとする必要があります。 学校で問題集を使っているのならそれを問題演習用にするとよいでしょう。学校で使うような問題集は現象、法則、解法パターンの解説が少ないので、ちょうどこの本で補完ができます。
投稿者 doraneco5675 : 14:21
物理のエッセンス
法則と問題の解法パターンの解説の後、問題演習という構成になっています。
解法パターンは癖がなく、うまくまとめられています。問題は1問1問狙いを持って選ばれた本質を突く良問です。また網羅度もこのレベルの問題集では一番高くなっています。
エッセンスをマスターすれば、入試問題を解くための準備は終わったと言ってよいでしょう。
この本の問題は入試問題を解くために必要な基本問題なので、なんとなく答えを出せるぐらいではなく、自分なりの視覚化・体系化の方法を使ってキチンと答えを出すことができるまでしっかりとマスターすることが大切です。
この本をメインに使う人でなくても、問題の解き方の手順がわかりやすくまとめられているので、解法マニュアルとして使えます。
投稿者 doraneco5675 : 14:17
らくらくマスター物理I・II
教科書例題レベルの問題が多く、物理が苦手な人でも使いやすい問題集です。
高認(大検)合格・中堅大学を目指す物理の苦手な受験生が解法パターンを習得するための本としておすすめします。
橋元はじめからていねいにや浜島の物理の実況中継と併用して理解度を高めれば、中堅大学で合格点を十分越えます。
ただし、この本は問題集の色合いが強く、これだけでは物理の視覚化・体系化が効率的に身につきません。中堅大学で高得点をとりたい、または、難関大学以上を目指すなら、解説が体系的な物理のエッセンスを使う方が良いでしょう。
投稿者 doraneco5675 : 14:07
橋元淳一郎の物理橋元流解法の大原則
物理を直感的に理解できるように、たとえ話を交えて解説をしています。
問題の解き方についても詳しく書かれていますが、分野によっては橋元さん独自の解説がされているところ(特に単振動)があるため逆に理解しにくいと思う人もいるでしょう。
基本的に、この本はクセがあります。無理に最初から最後までやるのではなく、概念がピンとこない所が出たらこの本を見て感覚的に理解する、という使い方がおすすめです。
もし橋元さんの問題の解き方がわかりやすいと思うのなら、最初から最後まで通してやっても良いでしょう。
投稿者 doraneco5675 : 13:59
浜島物理I・II講義の実況中継
実況中継シリーズの長所である<話し言葉での講義>なので、教科書レベルを軽くやっただけの人でも読みやすくなっています。
この本の問題と物理のエッセンスの問題は重複しているので、話の流れをこの本で押さえてから物理のエッセンスを使うと効果的です。
投稿者 doraneco5675 : 13:53
橋元の物理をはじめからていねいに
まったく予備知識がない人でも理解できるように、初歩の初歩から現象、用語、法則、解法パターンを解説しています。
教科書や普通の初心者向けの参考書を読んでもさっぱりという人におすすめです。
この本が理解できなければ、物理をやっていくのは厳しいかも。
投稿者 doraneco5675 : 13:49
2005年03月25日
名問の森
物理のエッセンスの著者の浜島先生の本です。
入試標準レベルからやや難しめまでの典型的な問題に加え、難系のリライト的な問題、最近の入試傾向にあった問題も掲載されていて網羅度はとても高くなっています。
解答もこのレベルの問題集としては、ていねいにわかりやすく書かれています。
ただ、この本は物理のエッセンスをやった人のための入試用問題集的な位置づけなのか、問題の解法パターンや現象・法則についての導入部分の解説があまりないのが残念です。 (名問の森に限らずこのレベルの問題集に共通することですが・・・)
投稿者 doraneco5675 : 14:33
2005年03月16日
微積が受験物理で役に立つ分野
高校で習う微積がどこで役に立つかをまとめました。参考にしてください。問題を解くときに微積が役に立つ分野
- 単振動
位置・速度・加速度・時間を求める
二体問題(ばねの両端におもりをつけて振動させる)を解く
- 交流回路
抵抗・コイル・コンデンサーの定義を知っていればリアクタンス・位相差などを覚える必要がなくなる
(詳しくは、微積を使う交流回路を見てください)
たとえば、単振動:mx" = -k x の一般解がx = a sinωt + b cosωtとなることを知っていれば、初期条件を与えることで、任意の時刻の位置、速度、加速度を求めることができます。
解法パターンで解く場合は、力学的エネルギー保存則を使うので、任意の時刻での位置、速度を求めることはできません。
微積を使えば解法パターンを覚えなくても、数学的な操作で必要な物理量を一般的に求めることができます。
意欲がある人は微積を使って解く方法を研究することをおすすめします。
物理量を定義する、公式を導くときに微積が役立つ分野
- 力学全般
位置・速度・加速度の定義と計算
運動方程式の定義と計算
仕事の原理を導く、エネルギー保存則を導く
運動量の原理を導く
- 熱力学全般
熱力学第1法則(エネルギー保存則)の計算
→仕事を求める、ポアソンの公式を導く
- 電気回路
電流、回路素子の電圧、エネルギーの定義
回路のエネルギー保存則を導く
電磁誘導による誘導起電力を求める
これらは微積を使ったからといって簡単に問題が解けるようになるわけではありません。
たとえば、等加速運動の問題を解くときに微積を使った場合のメリットは、高校教科書で与えられている等加速運動の公式を覚えていなくても導けることであって、運動方程式を立てる段階で力を正確に図示できていなかったら問題は解けません。
しかし、微積を使うことにより高校物理ではあいまいになっている物理量の意味や公式と公式のつながりをキチンと理解することができます。また、状況設定が複雑なときに正しく法則(たとえば、エネルギー保存則)を立てることができるメリットがあります。
微分積分を使わないと解けない入試問題は存在するか?
受験物理に微分積分は必要か?で書いたように、高校の教科書では微分積分を使っていることをはっきりと書いていません。そのため、入試問題は微分積分を使わなくても必ず解けるようになっているので、「微積を使わないと解けない問題があるのでは」という理由で微積を使う必要はありません。
<注>
一部の大学ではごくまれに、上に書いた物理量、法則が微積を使って定義され導かれていることを知っておかないと解けない問題が出題されることがあります。
たとえば、微積を使わないで問題を解くためには、⊿tが非常に短い時間であるとき、⊿sin(ωt) = ω cos(ωt) ・⊿tという近似式を与える必要がある問題で、この近似式が与えられていない問題が出題されたことがあるそうです。
これぐらいは数3をやった理系なら分かっとけってことなんでしょうね。
このような問題に対応するには、⊿を使って定義される物理量、法則は微分・積分につながっていることを知っておく必要があります。
詳しくは、物理のための微積を参考にして下さい(ここに書かれていることを知っていれば充分です)。
投稿者 doraneco5675 : 00:07
2005年03月15日
受験物理に微積は必要か?
受験物理に微積は必要か?これは受験生が一度は考えたことがある問題です。この記事では、物理においてなぜ微積を使うのか?そして、受験生は微積を使うべきか?について考えていきます。
高校物理での微積の扱い
高校の物理の教科書では目に見える形で微積は使われていません。たとえば、厳密には速度は位置を時間tで微分したものと微分を使って定義します。
しかし、高校の物理の教科書には微積という言葉が使われず、瞬間の速度はΔr/Δtと定義されています(非常に短い時間Δtの間に物体が移動した量をΔrとしている)。
これは位置rを時間tで微分していると言っているのに等しいのですが、これが微分だとは高校の教科書には一言も書かれていません。
その結果として、この瞬間の速度の定義を平均の速度と同じものと勘違いしている高校生は多いのではないでしょうか。
他にも、微積を使わなければ厳密に説明できないことを、あいまいで天下り的に説明している部分がいくつかあります。
高校物理の教科書は、物理を厳密に記述するために必要な微積を使わずに、物理を体系化しているのです。それに従い多くの参考書では微積を使っていません。
「微積を使うべきかどうかの議論」の本当の論点
物理に微積を使うことは本質的には何を意味しているのかを考えていきます。高校物理で微積を使っている代表的な参考書である、駿台文庫「新・物理入門」の序文には次のことが書かれています。
高校生とりわけ受験生用に書かれた物理の参考書の大多数が、(中略)物理学の論理性と実証性を完全に無視し、天下りに書かれた「公式」なるもののバラバラな羅列を高々それらの当てはめのテクニックに終始している。
やみくもに丸暗記させられてきた「公式」なるものが、実は原理から論理的・数学的に導き出されるものであり、同時にまた、物理的現実をよく表す法則の一表現形式であることを納得したとき、初めてその面白さが分かる。
この序文に書かれている主張はまったく正しいと思います。これが微積を物理に使う意義だと私は思います。
わかりやすく言いなおすと、物理に微積をはじめとする数学を使うことは、定義を厳密にして物理を体系的に理解することなのです。
「微積を物理に使うべきかどうかの議論」の本当の論点は、「厳密な定義で物理を理解すべきかどうか」にあるのです。
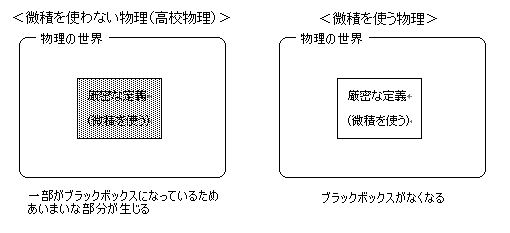
[図1]微積を使う物理と使わない物理のイメージ
受験物理と厳密な定義
受験物理において、厳密な定義を理解することが必要なのかについて考えていきます。まず私の考えを書きます。
厳密な定義を理解することが望ましい。しかし、受験の目標は限られた時間で合格に必要な問題を解けるようにすることなので、 時間対効果を考えた上で判断する必要がある。
考察するまでもないのですが、目標が物理の本質を理解することなら最初から微積を使って物理を理解することは有益です。しかし、受験本番までの時間は有限です。最初から厳密に理解しながら勉強するより短時間で効率的に得点力をつける方法があるのならそちらの方法をとるべきなのです。
以下では、この立場にたって受験生の学習段階別に考察をしていきます。
Case1 物理をまったく知らない~基礎固めをしている
このレベルの受験生は、現象・法則そのものを知らないので、どんな現象・法則があるのかを知る必要があります。
一般的に、知識がゼロに近い状態では抽象的な知識より具体的な知識のほうが理解しやすいことが知られています。
そのため、学習の初期段階では抽象的な厳密な定義を最初から学ぼうとするよりも、具体的な物理現象を通して現象・法則を理解していったほうが効率的だと考えられます。
Case2 入試対策をしている
このレベルになると、知らない現象・法則はほとんどなくなっているので、抽象的な厳密な定義を学ぶ準備はできているといえます。
しかし、準備ができているとしても、すべての受験生が微積を使って厳密な定義を学ぶべきかというと少し疑問があります。
それは次の疑問です。
・物理ができない原因は、微積を使っていないからだけなのか?
・普通の受験生が微積を使う物理に対応できるのか?
まずは、一つ目の疑問について考えてみます。
問題を解くときは、
・問われている現象を理解し、図で表す
・図で表した現象を式で表し、解く
という、ステップに分かれます。
微積が役立つのは図で表した現象を式で表し、解くというステップです。なぜなら、今までに書いてきたように法則の厳密な定義に微積などの数学が使われているからです。
「ということは、やっぱり微積は必要じゃないか!」という声が聞こえてきそうですが、私の経験だと、受験生が入試問題を解けない原因は、最初のステップができていない、つまり微積の能力とは無関係な読解能力の不足であることが多いです[図2]。受験物理では、状況設定が複雑でなければ二つ目のステップで迷うことはありません。
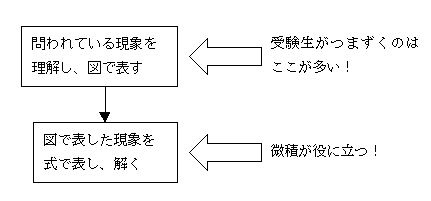
[図2]問題を解くときの手順
だから、微積を使う前に、まずは現象を図式化できるようにする必要があります。
次に、二つ目の疑問について考えてみます。
高校生が物理を始めるのは基本的には2年生からで、この時点で微積を使いこなせる人は少ないし、さらに単に微積の計算ができるだけでは微積を使って物理現象を理解することはできない、という問題があります。
これを解決するには、独学で数学の問題を解くための微積の知識だけではなくて、物理現象を理解するのに役立つ微積の直観的な見方を身につけることが必要になります。
詳しく知りたい人は、物理のための微積を参考にしてください。
以上のことを考えると、基礎が身についた受験生であっても、下の二条件を満たしていない段階では、微積は使わないほうがよいと思います。
・現象を的確に図式化できる
・物理現象を理解するのに役立つ微積の直観的な見方ができる
「先生や友達が微積が必要だと言っている」とか、「微積を使うと頭がよさそう」という理由だけで使うのはどうかと個人的には思います。
もちろん、上に書いた理由がきっかけで微積を使いたいと思う人が多いと思います。しかし、厳密な定義に基づく物理はパターンを暗記する物理と違って能動的な学習が求められます。上に書いた理由だけでこのような学習が続けられるか疑問に思っています(特に独学の人は)。
まとめ
- 高校物理では微積は使われていない
- 物理に微積をはじめとする数学を使うことは、定義を厳密にして物理を体系的に理解すること
- 微積そのものが抽象的でやさしい概念ではないので、物理を苦手にしている段階で無理に微積を使う必要はない
- 現象を的確に図式化することができ、微積の直観的な見方を身につけたら、微積は物理のストーリーを理解する助けになるので必要に応じて取り入れるとよい
投稿者 doraneco5675 : 23:05
オイラーの公式の使い方
大学に入ると次のような式を学びます。(e:自然対数)
この式はオイラーの公式と呼ばれています。この式を知っていると計算の見通しが良くなるので高校生でも知っておくと良いと思います。そこで、オイラーの公式を複素数に使いオイラーの公式の使い方について考えてみます。
複素数は、
Z=|Z|(cosθ+i sinθ)
と極座標(距離と角度)の形式で表すことができます。
このとき、Z1とZ2の積を考えると、
Z1×Z2=|Z1|(cos(θ1)+i sin(θ1))|Z2|(cos(θ2)+isin(θ2))
=|Z1||Z2|(cos(θ1+θ2)+i sin(θ1+θ2))
となります。
この式の図形的意味を考えると、
(Z1にZ2を掛ける)=(Z1を|Z2|倍に拡大)+(Z1をθ2回転)
というように解釈できます(これは複素数を図形的に考えるときに重要です)。
さて、ここからオイラーの公式を使うと役に立つ理由 を説明します。
上で積を考えたときに,計算で気になるのは、
(cos(θ1)+i sin(θ1))×(cos(θ2)+isin(θ2)) =cos(θ1+θ2)+i sin(θ1+θ2)
の部分です。 この式は、本来なら加法定理を利用して整理すべきものですよね。
しかし,オイラーの公式を使えば、
(cos(θ1)+i sin(θ1))×(cos(θ2)+i sin(θ2)) =(eiθ1)×(eiθ2)
=ei(θ1+θ2) (ea×eb=ea+bを使った)
=cos(θ1+θ2)+i sin(θ1+θ2) (オイラーの公式を使った)
このように指数関数の性質を使い簡単に計算することができます (加法定理の計算を指数関数の積にすることができた)。
また,オイラーの公式を使えばド・モアブルの式は、(eiθ)n = ei nθ という,指数関数の性質である(ea)b=eabのことを言っているだけだということがわかります。
最後にポイントをまとめます。
Z=|Z|(cosθ+i sinθ)をオイラーの公式を使いZ=|Z|eiθと表すと、めんどくさい三角関数の計算が指数関数の計算に変わるので計算が楽になる。
(指数関数の計算がめんどくさいから対数を取るのと、感覚的には同じ考え方)
オイラーの公式より、
オイラーの公式の複素共役を取ると、
{(1) + (2)}/2 よりcosが、 {(1) - (2)}/2i よりsinが次のように求まる。
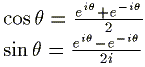
よって、三角関数は指数関数で表された。
投稿者 doraneco5675 : 22:17
ロピタルの定理の証明
h(x),g(x)が微分可能で,h(a)=g(a)=0のとき,
limx→a h(x)/g(x) = limx→a h'(x)/g'(x) が成立する
⇒h(x),g(x)が微分可能で,h(a)=g(a)=0のとき,
limx→∞ h(x)/g(x) = limx→∞ h'(x)/g'(x) が成立する
⇒h(x),g(x)が微分可能で,h(a)=g(a)=∞のとき,
limx→a h(x)/g(x) = limx→a h'(x)/g'(x) が成立する
ロピタルの定理は極限を求めるときに使われる定理です。
この定理を使えば、普通に解くと計算がめんどくさい不定形(0/0や∞/∞)の極限を簡単に求めることができます。
ロピタルの定理を使えばすぐ解けるような入試問題はまず出ないので実用性は低いのですが、一部の受験参考書でも紹介されている定理なので、とりあえず他の受験生に差をつけられないためにも知っておいたほうがよいと思います。
このページでは、問題を通してロピタルの定理の証明と使い方について簡単に説明をします。
ロピタルの定理は、高校教科書にある定義・定理だけを使って証明することができません。
たとえロピタルの定理が使える問題でも、検算に利用するだけにした方が無難だと思います。 実際、ここのページのように大学レベルの内容を使うことを良く思わない先生もいます。
1.h(x),g(x)が微分可能で,h(a)=g(a)=0のとき,
limx→a h(x)/g(x) = limx→a h'(x)/g'(x) が成立することを示せ.
2.h(x),g(x)が微分可能で,h(a)=g(a)=0のとき,
limx→∞ h(x)/g(x) = limx→∞ h'(x)/g'(x) が成立することを示せ.
3.h(x),g(x)が微分可能で,h(a)=g(a)=∞のとき,
limx→a h(x)/g(x) = limx→a h'(x)/g'(x) が成立することを示せ.
4.limx→∞x1/xを求めよ.
<準備>
ロルの定理
a<bとし、関数y=f(x)はf(a)=f(b)をみたすとする。
このとき、a<c<bをみたすあるcが存在して
f'(c)=0 が成り立つ。
ロルの定理は微分学の中心的な定理であり、高校で習う平均値の定理もこの定理から導かれます。
厳密な証明は難しいのでここでは詳しく書きませんが、f(a)=f(b)を満たす連続な関数f(x)のグラフを実際に書いてみれば、直感的にf'(c)=0を満たす点が存在することがわかります。
次に、ロルの定理からコーシーの平均値の定理を導きます。
コーシーの平均値の定理
h(x),g(x)が微分可能のとき、a<x<b内のある点cにおいて
h(b)-h(a) / g(b)-g(a) = h'(c)/g'(c) , a<c<b
が成立する。
ただし、(1)g(a)≠g(b)、(2)f'(x)とg'(x)はa<x<b内で同時に0にならないと仮定する。
[証明]
まず、F(x) = μh(x) - λg(x) として、F(a)=F(b)を満たす、μ,λを定める。
F(a)=F(b)
⇒μh(a) - λg(a) = μh(b) - λg(b)
⇒μ{ h(a) - h(b)} = λ{ g(a) - g(b)}
⇒λ= h(a) - h(b) , μ= g(a) - g(b)
よって、F(x) = { g(a) - g(b)} h(x) - { h(a) - h(b)} g(x) とする。
このとき、ロルの定理より、F'(c)=0が存在するので、
{ g(a) - g(b)} h'(c) - { h(a) - h(b)} g'(c) = 0
⇒{ g(a) - g(b)} h'(c) = { h(a) - h(b)} g'(c) - (*)
ここでg'(c)≠0。
なぜなら、g'(c)=0のとき、(*)より、仮定の(1)をふまえればh'(c)=0となるが、これは仮定の(2)に反する。
よって、(*)の両辺を{ h(a) - h(b)} g'(c)で割れば、
(*)⇒{ g(a) - g(b)} h'(c) / { h(a) - h(b)} g'(c) = 1
⇒h(b)-h(a) / g(b)-g(a) = h'(c)/g'(c)
を得る。(証明終わり)
以上で、ロピタルの定理を証明するための準備は終了です。
<解答>
1.
h(x),g(x)は微分可能で,h(a)=g(a)=0.
コーシーの平均値の定理より、
{h(x)-h(a)} / {g(x)-g(a)} = h'(c)/g'(c)
⇔h(x)/g(x) = h'(c)/g'(c) (☆)
x→a+0 のとき,c→a+0なので,
limx→a+0h(x)/g(x) =limc→a+0 h'(c)/g'(c)
を得る.
同様に,
limx→a-0h(x)/g(x) =limc→a-0 h'(c)/g'(c)
が成り立つ.
よって,
h(x),g(x)が微分可能で,h(a)=g(a)=0のとき,
limx→a h(x)/g(x) = limx→a h'(x)/g'(x)
が成立する.
2.
x=1/tと置き直すと,
limx→∞ h(x)/g(x)=limt→0 h(1/t)/g(1/t)
1.の結果より,
= limt→0 {(-1/t2)h'(1/t)}/ {(-1/t2)g'(1/t)}
= limt→0 h'(1/t)/g'(1/t)
= limx→∞ h'(x)/g'(x)
3.
h(x),g(x)は微分可能で,h(a)=g(a)=∞.
limx→a h(x)/g(x)=limx→a (1/g(x))/(1/h(x))
h(a)=g(a)=∞なので,1/g(a) = 1/h(a) = 0となり,1.の結果より,
limx→a (1/g(x))/(1/h(x))=limx→a (g'(x)/h'(x))×(h2(x)/g2(x))
⇔limx→a h(x)/g(x)=limx→a g'(x)/h'(x)×limx→ah2(x)/g2(x)
⇔limx→a h(x)/g(x)=limx→a g'(x)/h'(x)×(limx→ah(x)/g(x))2
limx→a h(x)/g(x)≠0のとき,
limx→a h(x)/g(x)=limx→a h'(x)/g'(x)
limx→a h(x)/g(x)=0のときは,0にならないように1を加えてから計算する.
つまり,
limx→a h(x)/g(x) +1=limx→a (h(x)+g(x))/g(x)
を考える.
上と同様にして,
limx→a (h(x)+g(x))/g(x)=limx→a (h'(x)+g'(x))/g'(x)
⇔limx→a h(x)/g(x) +1=limx→a h'(x)/g'(x) +1
⇔limx→a h(x)/g(x)=limx→a h'(x)/g'(x)
4.
log (x1/x) = log x/x
limx→∞ log x/x の値を求める.
limx→∞log x=∞,limx→∞x=∞なので,2.と3.の結果より,
limx→∞ log x/x =limx→∞ (1/x)/1=limx→∞ 1/x =0
よって,
limx→∞ log(x1/x)=0⇔limx→∞x1/x=1
投稿者 doraneco5675 : 22:16
科学の方法
科学的方法とその限界を具体例を交えて分かりやすく解説しています。物理学科を目指す受験生にぜひ読んでもらいたい一冊です。
「自然現象は数学のように明確で厳密なものである」という勘違いをしている受験生にもおすすめです。物理学の中でも体系的に説明できる部分を抜き出した高校物理しか学んでいない段階で、このような勘違いをするのは仕方ないことかもしれません。しかし、勘違いしたまま物理学科に行くと・・・。
投稿者 doraneco5675 : 21:55
図解雑学 微分・積分
微分・積分とはどのような考え方で、何に役立つのかをわかっていない人におすすめです。
この本を読めば、なぜ物理で微分積分が使われているのかがわかります。
同じ図解雑学シリーズ図解雑学 わかる微分・積分もおすすめです。
投稿者 doraneco5675 : 21:51
図解雑学 物理のしくみ
高校物理で習う分野を、身近な例を取り上げて図解をまじえて解説しています。
教科書や参考書に拒否反応がある人はこの本から読み始めましょう。物理に親しみがもてると思います。
投稿者 doraneco5675 : 21:48
参考書の選び方&使い方
・ 自分で分析・判断して参考書を選ぶ
参考書の選び方で失敗したくないという気持ちはわかります。
しかし、結果の責任は自分が持つのだから、人のアドバイスをそのまま受け入れるのではなく、自分でアドバイス、受験する大学の過去問、実力などを分析して選びましょう。
・ 今の自分の実力に合わせて参考書を選ぶ
自分の志望大学のレベルに合わせて最初からレベルの高い参考書を選んではいけません。まずは自分の実力を分析して自分がこなすことができる参考書から始めましょう。
あせって実力以上の参考書をやっても(気持ちはわかりますが)得るものはありません。
・ 自分との相性で参考書を選ぶ
著者が変われば、同じ現象・法則・問題でも説明の仕方が変わります。同じ説明でも受験生のレベルや性格によって合う合わないがあります。
人がすすめているから選ぶのではなくて、自分と相性の良い参考書を選びましょう。
・ 苦手な人は慎重に参考書を選ぶ
得意な人は参考書の解説が悪くても自分で補うことができます。
苦手な人はそれができません。苦手だと自覚がある人はできるだけ解説が詳しい自分にあった問題集・参考書を選びましょう。
・ 一度やる参考書を決めたらとにかくやってみる
使う参考書を決めた後で、「この本のレベルは自分にあっているだろうか?」、「この本だけで入試に対応できるだろうか?」など、いろいろ悩んでいるだけで参考書に手をつけない人がいます。
失敗したくないのでしょうが、やらなければ学力は絶対つきません。何もしなければ「参考書の選択の失敗」はしませんが、「受験の失敗」という大失敗をしてしまうことに気づいてください。
とりあえずやってみましょう。やっていくうちに、悩んでいたことの解決策が見えてきます。受験勉強は長いので「参考書の選択の失敗」ぐらいの失敗はすぐに挽回できます。
・ 参考書(講義)に使われない
分かりにくい部分があってもあくまで一人の著者(講師)にこだわる人がいます。
大切なことは、著書(講師)に義理だてることではなく、自分が内容を理解することです。分かりにくいと思うところがあったら、素直に別の参考書(講義)を使いましょう。
・ 学習法を間違えると良書も悪書になる
みんながすすめる参考書を使えば自然に力がつくと思っている人がいるかもしれません。しかしそれは明らかに間違いです。
自分で現象・法則の定義の意味を理解しながら参考書をマスターした人と定義をあいまいに理解したままでとにかく問題を解けるようにしただけの人とが同じように力がつくと思いますか?
(学習法について詳しくは、物理の学習法をどうぞ)
投稿者 doraneco5675 : 20:18
光速の物理
(注)旧課程の参考書です
本質を突きつつ盲点をチェックする問題が適切に選ばれています。
問題そのものの難易度は基礎から標準ですが、基本法則を正しく理解していないと解けません。
入試レベルの問題集を解く前のつなぎ、秋を過ぎてから直前期にかけて盲点チェック用に使うのがおすすめです。
問題数が44問と少ないので直前期でも十分使うことができます。
中堅大学を受ける人の入試対策にも適しています。
投稿者 doraneco5675 : 17:10
為近の基礎物理I・II
与えられた問題文から、どの解法を選択するのかを手順化していることが、この本の最大の売りです。
とりあえず問題文を読んで、たぶんこのパターンで解けるだろうという風に行き当たりばったりに解いている人、基本レベルと入試レベルの問題にギャップを感じている人におすすめです。
問題数は30題なので短期集中でやると効果的です。
中堅大学を受ける人の入試対策としても使えます。
投稿者 doraneco5675 : 16:55
2005年03月04日
理論物理への道標
定量的に問題を解いている本の中で最難関にある本です。
次の条件を満たしている人以外やる必要はないでしょう。というよりこの本をやろうとは思わないでしょう。
・超難関大学志望
・満点を取りたい
・本質が一番大事と思っている
・大学の物理に興味がある
投稿者 doraneco5675 : 22:20
SEGハイレベル物理
(注)旧課程の参考書です
微分積分などの数学を積極的に使っている問題集です。
テーマ別に講義と問題がセットになっていて、定量的な考え方を理解するだけでなく問題を解く実戦的な能力を身につけることができます。
最初から最後まで通して使ってもよいし、入試標準レベルの問題集をマスターした人がさらに得意にしたい分野だけを集中的にこなすのもよいと思います。
物理入門と違い、問題を解くための解説にも多少は重点が置かれているので、微積を使って厳密に考える方法を手早く身につけたい人はこちらをおすすめします。
投稿者 doraneco5675 : 22:11
新・物理入門問題演習
数学を使い問題を定量的に解くことを重視し、受験テクニックに頼るのではなく本質的に問題を解く方法を解説しています。
微積などの数学を積極的に使っていますが、問題は標準問題から始まっているので、意欲的な受験生ならなんとかやっていけるでしょう。
当たり前なのですが、数学を使って解く方法を身につけたい人は導出過程を自分で再現しながら進めてください。本にはあまり導出について詳しく書かれていませんが、それをしないと普通の解法パターン系の問題集をやっているのと同じになってしまうので・・・
投稿者 doraneco5675 : 22:10
難問題の系統とその解き方物理I・II―新課程
例題はやや難の問題が中心。練習問題は超難関大でも必要かどうかわからないハイレベルな問題まで掲載されています。
絶対的な力をつけるのに適していますが、すべての問題を解けるようにするにはかなりの実力と時間が必要になります。
普通の受験生が無理にやる必要はありません。特に直前気にやるべきではありません。
この本をやる価値があるのは、超難関大学で高得点を目指す人だけです(このレベルの受験生でも練習問題は不要)。それ以外の人は、入試標準問題を中心とした解説が詳しい問題集をやるほうが効率的です。
投稿者 doraneco5675 : 22:07
リンク → いろいろ
本・教科書を買う
辞書・百科事典
電話・郵便
旅行
相互リンク(受験・科学系以外)
夢はダッシュ村。
心の病を抱える家族とともに田舎暮らしをすることで、少しでも病気を良くしようと頑張っている。
InfoReview
Information Product(情報商品)のReviewサイト。
資格試験(国家資格)の資格取得リンク集
いろんな資格のリンクを掲載してます。
通販
総合通販価格チェッカー / 通販:売れ筋情報 / リストマニアSearch / 今日の売れ筋@Y
売れ筋情報(楽天)
グルメ / ドリンク / 花・ガーデニング / ペット・ペットグッズ / ゴルフ / 生活・インテリア / パソコン・家電・AV / キッズ・ベビー・マタニティ / ダイエット・健康 / 美容・コスメ・香水 / DVD・CD・楽器 / スポーツ・アウトドア / おもちゃ・ホビー・ゲーム / 車・バイク / ファッション
売れ筋情報(Amazon)
キッチン / 調理機器 / インテリア / 日用雑貨・生活家電 / 美容グッズ / 健康器具 /
セレクトショップ
北海道・東北 名産品お取り寄せ / 関東・信越 名産品お取り寄せ / 東海・北陸 名産品お取り寄せ / 近畿・中国・四国 名産品お取り寄せ/ 九州・沖縄 名産品お取り寄せ /
ブランド価格比較
エルメス / ルイ・ヴィトン / グッチ / クリスチャン・ディオール / コーチ / シャネル / プラダ / カルティエ / ティファニー / ブルガリ
投稿者 doraneco5675 : 20:50

 4.6点
4.6点 :橋元先生ありがとう!!
:橋元先生ありがとう!! 4.33点
4.33点

 3点
3点
 評価なし
評価なし











