ホーム > 物理の講義 > 電磁気
 « 電場・電位の概念（初心者用） | ０からはじめる磁気 | 微積を使う交流回路 »

０からはじめる磁気

目標

まったく磁気を知らない人でもわかるレベルで、磁気について解説します。

目標は、

この記事を読んだ後で問題集の解答を自力で理解できるようになること
自分なりに磁気を視覚化・体系化できるようになること

です。

電気の分野については、空がとっても青いからの大学受験・電気物理が参考になります。

磁気とはなにか？

磁石に他の磁石を近づけると、磁石は互いに引き合ったり反発したりします。

このような現象の根源となるものを磁気といいます。

磁気で働く力は、離れて(接触しないで)力が働く、引き合ったり反発したりする、という点で電気で働く力と類似しています。
電気の世界と対応させながら磁気の世界で何が力が生じる原因をつくるか、どんな力を受けるかについて説明していきます。

何が磁場をつくるか？～電場との比較

クーロンの法則～静電気力と磁気力との比較

電気におけるクーロンの法則とは、
２つの電荷が静止しているとき、静電気力の大きさFは二つの電荷の間の距離rの2乗に逆比例し、それぞれの電気量q₁および q₂に比例する
（→F=K(q₁q₂/r²)というものです。

これに対応するものが磁気に存在していて、磁気でのクーロンの法則は、
磁石の間に働く力を磁極(磁荷)間の力に基づくとみなすと、磁極間の磁気力も静電気力の場合と同様に距離の2乗に逆比例し、それぞれの磁極の磁気量m₁およびm₂に比例する
（→F=K'(m₁m₂/r²)というものです。

このように磁気と電気は対応関係にあるので電気で使われた理論が磁気でも同じように使うことができます。

電気の世界では、力Fは電荷qと電場Eを用いて、
F = qE
と表されます。
また、電場の様子は電気力線を使って表されます。

磁気と電気は対応関係にあることをふまえれば、
磁気の世界では、力Fは磁荷mと磁場Hを用いて、
F = mH
と表されると推測できます。
このとき、磁場の様子は磁力線で表されます。

電気と磁気の対応関係
電荷q ⇔ 磁荷m
電場E ⇔ 磁場H
電気力線 ⇔ 磁力線

このような類推は確かに正しいのですがひとつ疑問点があります。
磁荷とはなんなのでしょうか？

電荷はこの世に存在するどんな物質にも含まれています。ガラス棒を絹布で摩擦すると物質は電荷を持つようになる、ということを習ったことがあると思います。

一方、磁荷を取り出す方法を習ったことがあるという人はいないでしょう。
実は、磁荷というものは存在しないからです。

磁石にはN極とS極が存在しています。これは、電荷で言えばプラスとマイナスの電荷に対応するものです。

もし、磁荷が存在しているなら、磁石を細かく切り刻むことにより、単独でN極とS極が表れるはずです。
しかし、磁石をどれだけ細かく切っても、切った端にN極とS極が表れ、単独でN極とS極を得ることはできません。
つまり、磁荷を見つけることができないのです。

では、磁荷が存在しないのなら、何が磁場をつくっているのでしょうか？

＜参考＞磁極
磁極はそういうものがあったほうが都合がよいという事情からできた概念であって現実には存在しません。そのため磁気力のクーロンの法則は、現象論的な法則とみなされています。
しかし、電磁気学の体系自身は磁極が単独で存在できる形になっているし、宇宙に単独の磁極が存在する可能性もないわけではありません。その意味では磁気力のクーロンの法則は、電気力の場合と同じ資格の基礎法則といえます。

何が磁場をつくるのか？

まず、次の問題を考えてください。

<問題>
磁石を細かく切っていけば、つぎつぎと磁石を作ることができる。では、磁石を細かく切る回数に限界はあるか？

答えは、「切る回数に限界はある」です。
磁石を原子(陽子や電子)にまで細かく刻んでしまうと、これ以上は切ることができません。
一番小さい磁石は、原子なのです。

原子では、プラスの電気を持った陽子のまわりでマイナスの電気を持った電子が回転しています。
実は、この電子の回転が磁場をつくる正体なのです。
磁場は、磁荷がつくるのではなく、動いている電荷がつくるのです。

磁場のつくり方

繰り返しますが、動いている電荷が磁場をつくります。

つまり、
電荷が動く　→　磁場が生じる
という因果関係が成立しています。

では、電荷が動くと磁場はどのようにつくられるのでしょうか？

磁場が生じる原因となる電荷の動かし方によって、磁場の生じ方は変わるので、電荷の動かし方で分類します。
（２つの現象に因果の関係があるとき、原因の部分を変えれば結果が変わるだろう、と考えるのは自然な考え方ですよね）

受験では、下の３つの電荷の動かし方しか出ないので覚えてください。

注意　以下では、電荷の集団が動くとき、つまり、電流を流したときに生じる磁場について考える。

＜Case 1＞　電荷を直線に動かす（直線電流）
電荷を直線に動かす（直線導線に電流 I [A]を流す）と、直線導線から半径r [m]離れたところに[図１]のように磁場 H(大きさ= I / 2πr)が生じる。

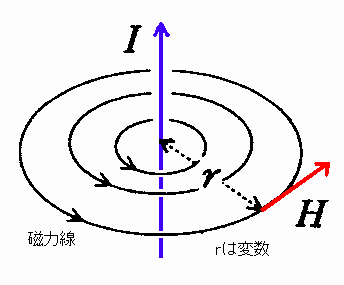
[図１] 電荷を直線に動かす（直線電流）

＜Case 2＞　電荷を円形に動かす（円形電流）
電荷を円形に動かす（円形導線に電流 I [A]を流す）と、半径r [m]の円形導線の中心で[図２]のように磁場H(大きさ= I / 2r)が生じる。

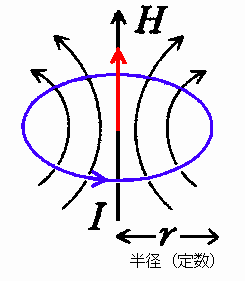
[図２] 電荷を円形に動かす（円形電流）

＜Case ３＞　電荷をソレノイドに沿ってに動かす
電荷をコイルに沿って動かす（ソレノイドに電流I [A]を流す）と、ソレノイドの中心で[図３]のように磁場H(大きさ= n I )が生じる。

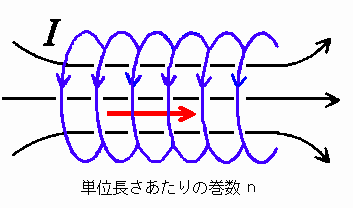
[図３] 電荷をソレノイドに沿ってに動かす

磁場の向きは、[図４]のように、右ねじを回す向きを磁場Hの向き、右ねじを回すと進む向きを電流Iの向き、と考えればどんな電荷の動かし方の場合でも求めることができます。

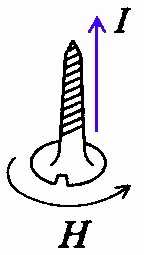
[図４] 右ねじの法則

磁束密度Bと磁場Hの関係

磁場の作用で物体が磁石になる現象を磁化といいます。
磁化に注目すると、磁束密度Bと磁場Hには下のような違いがあることがわかります。

磁束密度Bは磁化のしやすさを含む値
磁場Hは磁化のしやすさを含まない値

このとき、磁化のしやすさを表すものとして、透磁率μを使うと、
B=μH
という式が成立します。

磁場での現象は磁化のしやすさも関係するため、磁場Hではなく磁束密度Bで考える必要があります。
さらに詳しい話は、大学レベルの話になるのでここではふれません。

磁束密度Bの別の意味については、電磁誘導のところで説明します。

磁場から受ける力

電場では、電場に電荷を置くと電場から力を受けます。
磁場に電荷を置いても磁場から力を受けません。

では、どうすれば磁場から力を受けるのでしょうか？

その答えは次の実験結果からわかります。

＜実験＞

磁石で作った磁場の中に電線を置き、電流を流さないときと電流を流したときの電線の様子を観察する。

＜結果＞
電流を流さないとき、電線に変化はなかった。
一方、電流を流したとき、電線が曲がった。[図５]

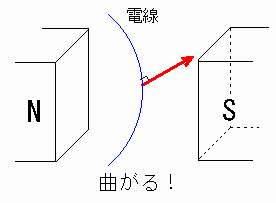
[図５] 磁場で電荷を動かす

この実験の結果から、磁場に電荷を置いただけでは磁場から力を受けないが、電荷を動かす（電流を流す）と磁場から力を受けるということがわかりました。

電荷の数で分類して、磁場から受ける力を２種類に分けます。

＜Case 1　電気を帯びた粒子（荷電粒子）が動く＞
電荷 q [C]の荷電粒子を速度 v [m/s] で動かすと、[図６]のように速度vから磁場 Bの向きに右ねじを回したとき進む方向に大きさF=qvB の力を磁場から受ける。この力をローレンツ力という。（ただし、速度 vと磁束密度 Bは直交）

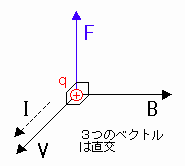
[図６] 荷電粒子が受ける力

（注１）電荷 q が負のとき、力Fの向きは逆になる。（注２）速度 vと磁場 Bが直交でないとき、速度 vか磁束密度 Bの垂直になる成分を取る。[図７－１]、[図７－２] このとき、どちらで計算しても当然同じF=qvB sinθとなります。

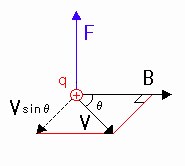
[図７－１] 速度の垂直成分をとる

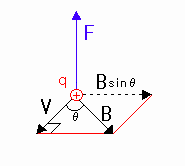
[図７－２] 磁束密度の垂直成分をとる

＜Case ２　電流が流れる（荷電粒子の集団が動く）＞
導線の長さが l[m]の導線に電流 I を流すと、[図６]のように電流I から磁束密度 Bの向きに右ねじを回した方向に大きさ F=IBlの力を磁場から受ける。この力を電磁力という。（ただし、電流 Iと磁束密度 Bは直交）

（注１）電流 I と磁束密度 Bが直交でないときは、電流 I の垂直成分は取れないので、[図７－２]のように磁束密度の垂直成分をとる。このとき、F=I(B sinθ)l
（注２）電磁力は導線内に存在する電子が受ける力の和なので、
（電磁力）＝（導線内に存在する電子の総数）×（ローレンツ力）
が成立している。（この証明はできるようにする）

電磁誘導～磁場から電場をつくる

今から、電磁誘導という現象について考えていきます。まずは、準備として磁束密度、磁束線、磁束について説明します。

磁束密度と磁束線の関係

磁束密度と磁束線を関係づけるために、次のように定義します。

定義：磁束密度と磁束線の関係
磁束密度 B のとき、1 m²あたりにB本の磁束線が面を垂直に貫くとする。[図８]

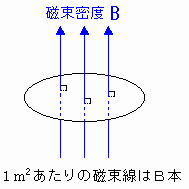
[図８]　磁束密度と磁束線の関係

磁束Φ(磁束線の総数)

ある領域Ｓ（面積Ｓm²）に存在する磁束線の総数を磁束Φ、とよぶ。
このとき、定義（磁束密度と磁束線の関係）より、
磁束Φ（磁束線の総数）＝Ｂ×Ｓ
（ただし、磁束線と磁束線を貫く面は垂直（注））[図９]

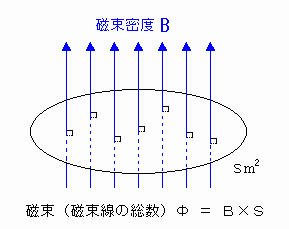
[図９]　磁束

（注）磁束線と磁束線を貫く面が垂直でないとき、定義のように磁束線と面が垂直になるように面の垂直成分[図１０－１]または磁束密度の垂直成分[図１０－２]を取る。

面の垂直成分を取る

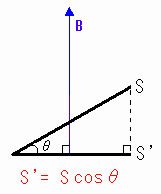
[図１０－１]　面の垂直成分をとる

このとき、磁束Φ＝Ｂ×Ｓ’＝Ｂ×Ｓcosθ

磁束密度の垂直成分をとる

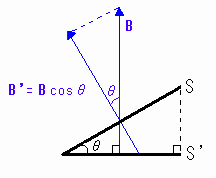
[図１０－２]　磁束密度の垂直成分をとる

このとき、磁束Φ＝Ｂ’×Ｓ＝Ｂcosθ×Ｓ

当たり前ですが、どちらの垂直成分をとっても磁束Φの値は変わりません。

● 電磁誘導とはなにか？

「何が磁場をつくるのか？」で説明したように、
電荷を動かす　→　磁場が生じる　-(*)
という現象が起きるのならば、

逆の現象、つまり、
磁場を生じさせる　→　電荷が動く -(**)
が起きるのではと考えられます。

実験により、確かに(**)が起きることが確認されました。
この現象を電磁誘導と呼びます。

さて、磁場を生じさせるとはどういうことでしょうか？

調べてみると、
磁場を生じさせる＝磁束Φを時間に対して変化させる　-(***)
ということがわかりました。

(**)と(***)をまとめて、電磁誘導とは、
磁束Φを時間に対して変化させる　→　電荷が動く
ということと言えます。

電荷が動くということは、本質的には電場が生じているということ。つまり、電磁誘導とは磁束Φが時間的に変化させると電場が生じる現象、といったほうが正確です。

電磁誘導の意味

電磁誘導とは、磁束を時間に対して変化させると電荷が動くという現象です。
では、電荷が動くと何が起こるのでしょうか。

そこで、磁束密度 Bの場所で導体棒を動かす場合を考えてみましょう。

[図１１]のように導体棒を磁束密度 Bに対して垂直な方向に速度 vで動かす（Φ＝ＢＳのＳの部分を時間に対して変化させる）と、[図１２]のように電荷が動き陽子と電子がそれぞれ導体棒の端に移動する（陽子、電子の動く向きはローレンツ力で説明できる）。

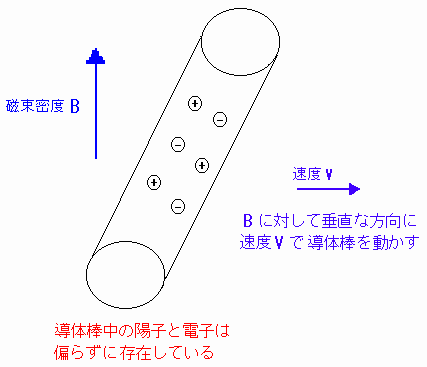
[図１1]　導体棒を磁場で動かす

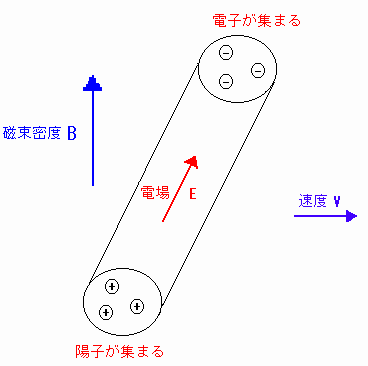
[図１２]　磁場で導体棒を動かした後の状態

このとき、電荷が動くことにより、導体棒内で電場 Eが生じ、電位差が生じる。

電位差が生じているので、[図１３]のように導体棒は電池化したと考えることができる。

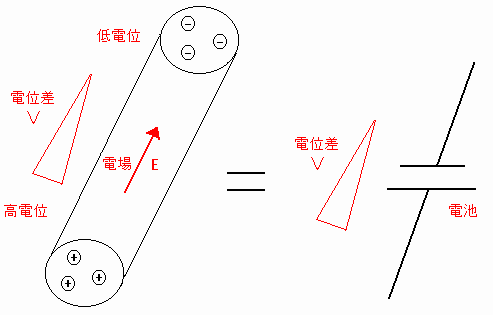
[図１３]　導体棒の電池化

よって、電磁誘導とは導線（コイル）が電池化すること、といえる。
このとき生じる電位差Ｖを誘導起電力と言います。

ちなみに、導体棒に生じる誘導起電力は、後で説明するファラデーの法則を使わなくても、今までの知識で次のように求めることができます。

＜ローレンツ力による電磁誘導の解釈＞

電子の電荷をe、導体棒の長さをlとする。
電子が受ける力は、磁場からの力と電磁誘導が起きたことにより生じた電場からの力を受けます。そして、電子は端で止まっているので、磁場からの力（ローレンツ力）と電場による力はつりあっていることがわかります。
よって、
（電場から受ける力の大きさ）＝（磁場から受ける力の大きさ）
→ｅＥ＝ｅ v Ｂ
→Ｅ＝ｖＢ　-(*)

また、導体棒内では一様な電場が生じているので、
（電位差）＝（電場の大きさ）×（導体棒の長さ）
→Ｖ＝Ｅｌ　
が成立。
(*)を代入して、
誘導起電力Ｖ＝ｖＢｌ
このとき、速度 vから磁束密度 Bの向きに右ねじを回したときにねじの進む向きが高電位となっています。

誘導起電力の求め方（ファラデーの法則）

一般にコイルの誘導起電力を求めるために、ファラデーの法則とレンツの法則を使います。

ファラデーの法則は、
誘導起電力｜Ｖ｜＝｜ΔΦ／Δｔ｜
であり、これから誘導起電力の大きさが求まります。

レンツの法則は、
磁束Φの変化を妨げる方向に誘導起電力は生じる（自然は変化を嫌う）、
というもので、これから誘導起電力の向きが求まります。

このふたつの法則を合わして、
誘導起電力Ｖ＝－ ΔΦ／Δｔ　（マイナスの符号がレンツの法則を表している（注））
と表して、これを普通はファラデーの法則とよびます。

ただし、微積を使わないで誘導起電力を求めるときは、誘導起電力の大きさと向きは別々に求めるので、誘導起電力の大きさを決めるのがファラデーの法則、向きを決めるのがレンツの法則と理解したほうが初心者の人にはよいと思います。

（注）マイナスの符号がレンツの法則を表す理由
コイルと同じ形の円形電流[図２]を見てください。
電流の流れる向きを右ネジをまわす向きとすると、右ネジの進む向きに磁場が生じています。このとき、右ネジが進む向きに回す方向の起電力を正とします。

レンツの法則によれば、磁束Φが増加するとき、右ネジが戻る向きに回す方向が高電位となる誘導起電力が生じます。これは、先ほど定義した起電力の向きとは逆なので、マイナスがつきます。
どうやって誘導起電力の向きが決まるかは、次の誘導起電力の向きが決まる仕組みを見てください

（補足）

微積を使えば、誘導起電力Ｖは、
Ｖ＝－ｄΦ／ｄｔ
と表される。

微積を使えば誘導起電力の大きさと向きを別々に考える必要がなくなり機械的に解けるので、数学が得意な人は使ってみるのもいいかもしれません。
ただし、回路方程式の立て方（ループの向き、電流の向きの設定方法、回路方程式での電池・回路素子の符合の決め方）を分かっていないといけません。

最後に、誘導起電力の向きの決め方を確認します。

＜誘導起電力の向きの決まる仕組み＞
誘導起電力が起きる仕組みは次のようになっています。

レンツの法則より、
磁束Φが増加（減少）したとき、
磁束Φの増加（減少）を妨げるために(I)の向きに磁場Ｂ’が生じる。
（磁束Φ＝ＢＳなので、磁束の変化と逆向きに磁場Ｂ’をつくれば、磁束の変化と逆向きに別の磁束が生じ、磁束の変化を妨げることができる）
このとき、磁場Ｂ’を作るためには、(II)の向きに電流を流せばよく、(II)の向きに電流が流れているとき、コイルに(III)のような電池があると仮想できるので、誘導起電力は(III)のようになる。［図１４］

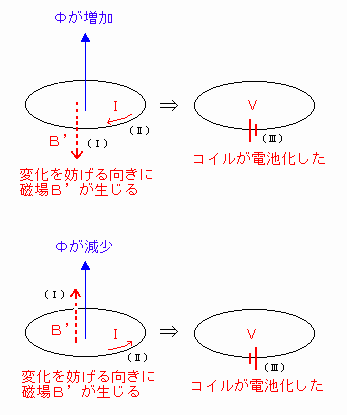
［図１４］　誘導起電力の向き

ホーム > 物理の講義 > 電磁気
 « 電場・電位の概念（初心者用） | ０からはじめる磁気 | 微積を使う交流回路 »

投稿者猫背の狸、更新日 2006年12月30日

０からはじめる磁気

目次

目標

磁気とはなにか？