ホーム > 物理の講義 > 物理のための数学
 « 物理のための微積 | 物理のためのベクトル | 物理のための三角関数 »

物理のためのベクトル

目標

ベクトルは物理の世界を理解するための道具として大切なものです。
しかし、物理の初心者は、数学としてはベクトルを知っているけれど、物理にベクトルを適用することができないことが多いのです（微積についても同じことが言えます）。これでは物理の体系を効率的に理解することができません。

そこで、この記事では数学にでるベクトルの問題を解くための解説ではなく、どうして、どうやって物理にベクトルを使うのかの解説をします。

ベクトルとは何か？

物理では、物理量（測定により得られる量）を表すために、数学の言葉で言う、スカラーとベクトルを使います。
ここでは、スカラーとベクトルの定義をし、ベクトルの表し方、スカラーとベクトルの違いについて説明します。

● スカラーとベクトルの定義
スカラーとベクトルは次のように定義されています。

大きさのみを表すものをスカラー
大きさ＋向きを表すものをベクトル

● ベクトルの表し方
ベクトルは[図１]のように、

矢印の長さ=大きさ
矢印の先の向き＝向き

として表される。

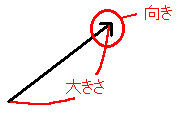
[図１]ベクトルの表し方

● スカラーとベクトルの違い
スカラーとベクトルの違いは、スカラーは向きを示すことができないのに対して、ベクトルは向きを示すことができることです。
この違いを理解していないと、物理量を正確に表すことができなくなります。

なぜベクトルを使うのか？

スカラーとベクトルの違いについては「ベクトルとは何か？」で紹介しました。
では、なぜベクトルを使わなくてはならない場合があるのでしょうか？
次の例題を考えてみてください。

<例題>

ＡとＢの距離は5km
Ａから見てＢは北東にある

このときスカラーで考えたとき、ベクトルで考えたとき、それぞれＡから見てＢはどこにあるかを図示しなさい。

<解答>
まず、条件が何を表しているかを考えます。
１は大きさ（距離）についての情報
２は向きについての情報

このことをふまえて、スカラーの場合、ベクトルの場合をそれぞれ考えて行きましょう。

スカラーで考える
スカラーは大きさのみを表すので、１の情報しか使うことができない。
１より、ＢはＡを中心として半径5Kmの円上のどこかにある[図２]。
（２の情報が使えないのでこれ以上Ｂの位置はわからない）

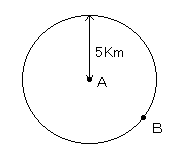
[図２]大きさの情報によるＢの図示

このように、スカラーで考えると、Ｂの位置を完全に確定することができない。
→位置を表すのにスカラーは不適である！

ベクトルで考える
ベクトルは大きさ+向きを表すので、１と２の両方の情報を使うことができる。

まず１より、Ａを中心とした半径5Kmの円上にＢが位置していると考える事ができる[図２]（ここはスカラーと同じ）。

次に２より、ＢはＡからみて北東の向きにあることから[図３]の矢印上のどこかにＢが位置していると考えることができる。

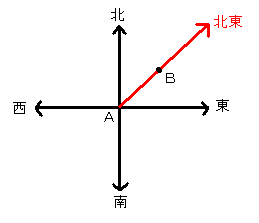
[図３]向きの情報によるＢの図示

よって、[図２]と[図３]をあわせて考えれば、
Ｂは[図２]の円と[図３]の矢印の交点として求まる[図４]。

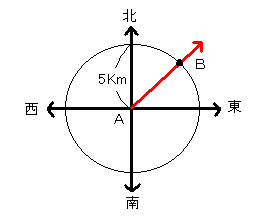
[図４]大きさ＋向きの情報によるＢの図示

このようにベクトルで考えるとＢの位置を正確に定めることができるわけです。つまり、位置を表すのにベクトルは適しているのです。

例題の結果を考えれば、
位置を示すときにはベクトルを使わないと正確に示す事ができないということが分かります。

物理では位置を含めてベクトルを使わないと正確に示すことができない物理量がいくつか存在します（だから物理ではベクトルが必要になる）
（例）位置、速度、加速度、力、・・・

c.f.ベクトルを使わなくても、つまりスカラーで正確に示すことができる物理量もいくつか存在している。
（例）質量、時間、・・・

物理が苦手な人は、ベクトルとスカラーの区別をしていない人が多いので、問題を解くとき物理量はベクトルで表すのか、スカラーで表すのかを意識するようにしましょう。これが物理を得意科目にする第一歩です。

ベクトルの性質

ベクトルの性質について確認します（詳しくは、自分の使っている数学の参考書で確認してください）。

ベクトルがまったくできない人は予備校講師鴫原の部屋（別館１）の「高校で学べない人のための、ベクトル」が参考になります。

ベクトルは、大きさと向きを使いどの向きにどれだけ移動したかを表します。ベクトルを表示するためには矢印が使われます。

例えば、[図５]の点Ａから点Ｂまでの移動量をと書いてベクトルＡＢと読み、出発する点Ａを「始点」、到着する点Ｂを「終点」といいます。

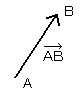
[図５]ベクトルＡＢ

ベクトルは向きと大きさで決まる量なので、２つのベクトル

と

について、

＝

となるのは、[図６]のように、移動量が同じ、つまり、向きと大きさが同じときに限ります。すなわち、２つの矢印が平行移動で重なるとき、この２つのベクトルは等しいというのです。

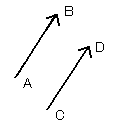
[図６]等しいベクトル

また、２つのベクトル

と

について、

＝－

となるのは、[図７]のように、移動量が反対、つまり、向きが反対で大きさが同じときに限ります。すなわち、２つの矢印が平行移動で反対向きに重なるとき、この２つのベクトルの正負が逆になるのです。

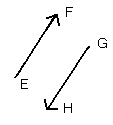
[図７]正負が逆のベクトル

さて、ここからはベクトルの合成、分解について説明します。

次の関係が成り立つのは明らかですよね[図８]。
（点Ａから点Ｂまでの移動量）＋（点Ｂから点Ｃまでの移動量）
＝（点Ａから点Ｃまでの移動量）

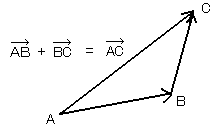
[図８]点Ａから点Ｃへの移動

これをベクトルを使って書けば次のようになります。
＋＝ -(*)
これをベクトルの合成といいます。

一方、(*)を逆から見ると
＝＋ -(**)
これをベクトルの分解といいます。

このように、ベクトルでは、
２つ以上のベクトルを”つないで”１つのベクトルに合成
１つのベクトルを”わけて”２つ以上のベクトルに分解
することができるのです。

物理にベクトルを使うときに役に立つのは、１つのベクトルを”わけて”２つ以上のベクトルに分解できるという性質です。
この性質のおかげで、ベクトルを座標表示することができ、ベクトルを数式として処理する事ができるようになるのです。

これについては次の「ベクトルの座標化」で説明します。

ベクトルの座標化

ある点の位置はベクトルを使って[図９]のように図で表すことができます。

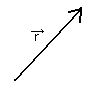
[図９]位置ベクトル

これを式で表すと

と書くことできます。しかし、

は[図９]の矢印の代わりになっているだけで、ベクトルを含んだ計算を行うときのままでは考えにくいのです。

だから、図であるベクトルを数式化し計算を行いやすくするために、座標を導入する必要があるのです。
→座標は図形問題を計算問題に変換する働きをする

ベクトルの座標表示の方法をPointにします。

＜Point＞ベクトルの座標表示の方法

座標は必要に応じて自由に取り入れることができる -(*)

原点を決める（注）
すべてのベクトルが｛直線上、平面上、空間上｝に存在するとき、
座標軸を｛１本、２本、３本｝導入する
ベクトルを座標軸上に分解する
それぞれの軸について、
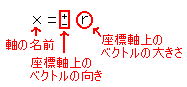の型で表す

（注）位置ベクトルの始点は原点と一致させる。

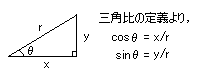
上のPointをふまえて、[図９]の位置ベクトル（大きさはr）に座標を導入してみます。

位置ベクトルが直線上にあるとき、[図１０]のようにベクトルと同じ向きを正として座標を導入すると、下のようにベクトルを数式化できる。

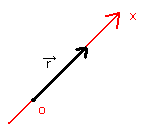
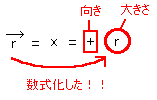
[図１０]座標の導入例１

位置ベクトルが直線上にあるとき、[図１１]のようにベクトルと逆の向きを正として座標を導入すると、（[図１０]のときと座標の正の向きが逆）下のようにベクトルを数式化できる。

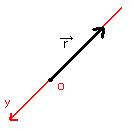
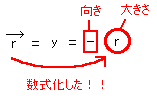
[図１１]座標の導入例２

位置ベクトルが平面上にあるとき、[図１２]のようにわざとθの角をなすように座標を導入すれば（座標は自由に取り入れる事ができる（普通は計算しやすいように座標を導入する））、下のようにベクトルを数式化できる。

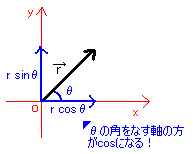
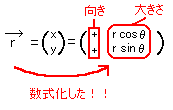
[図１２]座標の導入例３

（上のようにベクトルが分解できることは覚えておく！（理由は下の三角比の定義を見ればわかります））

<三角比の定義>

さらに詳しくは、物理のための三角関数を参考にしてください。

このように、ベクトルを座標表示すれば、ベクトルは数式化され物理の問題に適用しやすくなるのです。

物理が苦手な人は、ベクトルで表される物理量を扱っているときに、スカラーとベクトルの区別ができていない（ベクトルとわかっていない）ので、ベクトルの座標表示をすることができないのです。

そのために、放物運動、鉛直投げ上げ、鉛直投げ下げ、自由落下などの落体の運動を解くときに、お互いを関連づけることができずしかも公式として暗記してしまうのです。位置、速度、加速度がベクトルであることをわかっていれば、ベクトルの座標表示を使えば公式として暗記する必要が無くなることがわかるはずです。

落体の運動を公式として暗記している人は、等加速度直線運動の式

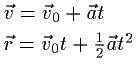
に座標表示した初速度、加速度を代入すれば、公式を暗記しなくても導ける事を確認してみてください。

まとめ

物理量はベクトル（大きさ+向き）かスカラー（大きさのみ）で表される
ベクトルとスカラーの区別をしないと物理量は正確に表すことができない
ベクトルは座標表示して数式化して計算する