ホーム > 物理の講義 > 物理のための数学
« 物理のためのベクトル | 物理のための三角関数

物理のための三角関数

物理で必要になる三角関数関係の公式をまとめました。
ここに出てくる公式、公式の導き方はすぐに使えるようにしましょう。
この程度は押さえていないと、参考書を読むのも大変だと思います。

●三角比の定義と定理

[図１]のような角度θ[°]をとる直角三角形において、

sinθ= a/c
cosθ= b/c
tanθ= a/b

と定義する。

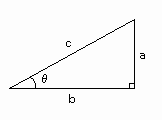
[図１]　三角比の定義

また、定義から次の二つの定理が成り立つ。

tanθ= sinθ/cosθ
（証明）
tanθ=a/b
=(a/c)/(b/c) ←分母分子をcで割った
=sinθ/cosθ←sin,cosの定義を代入した

sin²θ+cos²θ=1
（証明）
sin²θ+cos²θ
=(a/c)²+(b/c)²=(a²+b²)/c²
ここで、三平方の定理より、
a²+b²=c²が成立するので、
sin²θ+cos²θ=1

●余弦定理

[図２]のような三角形において、

a²=b²+c²-2bc cosθ
が成立する。

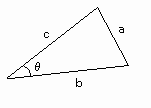
[図２]　余弦定理

●三角関数の定義と定理

[図３]のように半径１の円で(1,0)から逆時計回りに弧長θ[rad]をとったとき、
その円上の点のy座標をsinθ、x座標をcosθと定義する。

sinθ=y
cosθ=x

また、原点と点(x.y)を通る直線の傾きをtanθと定義する。

tanθ= y/x

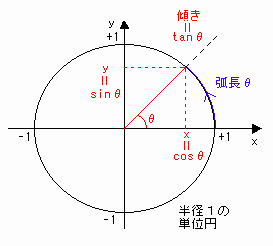
[図３]　三角関数の定義

＜三角関数を導入した理由＞
三角比ではθは度（長さではない単位）を、三角関数ではθは弧長（長さ）を基準とした定義です。 物理ではθが変化する、つまりθを変数とする関数が必要になる場合が出てきます。 しかし、関数は長さを持つものでないと変数として使いにくいので、三角比を三角関数に拡張する必要があります。

＜弧度法の定義＞
[図４]において、弧長＝半径×θ[rad]（←弧度法の定義）なので、半径１の単位円では弧長＝θ[rad]となります。
θ[rad]は、π[rad]＝180[°]の対応関係が成り立つことから、θ[rad]/π[rad]＝θ[°]/180[°]が成り立つことを使って求めています。

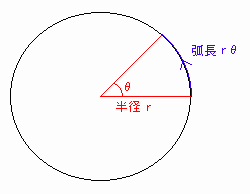
[図４]　弧度法の定義

＜円のパラメータ表示＞
三角関数の定義を、半径ｒの円に拡張すれば、
（ｘ、ｙ）＝（ｒ cosθ、ｒ sinθ）
となります。
円のパラメータ表示は三角関数の定義を拡張したものなので、ｘ座標sinをｙ座標cosとすることはできません。

また、定義から次の二つの定理が成り立つ。

tanθ= sinθ/cosθ
（証明）
tanθ=y/x←(0,0)と(x.y)を通る直線の傾き
=sinθ/cosθ←sin,cosの定義を代入した

sin²θ+cos²θ=1
（証明）
sin²θ+cos²θ
=x²+y²
ここで、(x,y)は半径１の単位円上の点なので、
x²+y²=1が成立する。
よって、
sin²θ+cos²θ=1

また、単位円を使えば、

sin(-θ)=-sinθ
cos(-θ)=cosθ
tan(-θ)=-tanθ

sin(π/2-θ)=cosθ
cos(π/2-θ)=sinθ

を得る。

これらの式は、単位円を使って左辺の値は+sinθ、-sinθ、+cosθ、-cosθのいずれに等しいかを考えれば求めることができる。

また、tanについては、tan=sin/cosから求めることができる。

●加法定理

sin(α+β)=sinαcosβ+cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
また、tan(α+β)=sin(α+β)/cos(α+β)より、
tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)
（証明）
tan(α+β)=sin(α+β)/cos(α+β)
=(sinαcosβ+cosαsinβ)/(cosαcosβ-sinαsinβ)
=((sinα/cosα)+(sinβ/cosβ))/(1-(sinαsinβ)/(cosαcosβ))←分母分子をcosαcosβで割った（tanが出てくる形にしたいから）
ここで、tan=sin/cosを使えば、
tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)となる。

また、
・β=-βとすれば、
sin(α-β),cos(α-β),tan(α-β)を得る。

・α=βとすれば、
二倍角の公式、半角の公式を得る。

・Ａ=α+β、Ｂ=α-β⇒α=(Ａ+Ｂ)/2、β=(Ａ-Ｂ)/2とすれば、
和・差の変形公式を得る。

●合成公式

a sinθ + b cosθ =√(a²+b²) sin(θ+φ) (tanφ=b/a)
ただし、φは[図5]を満たすφである。

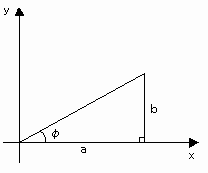
[図５]　合成公式

ホーム > 物理の講義 > 物理のための数学
« 物理のためのベクトル | 物理のための三角関数

投稿者 猫背の狸 、更新日 2006年12月30日