ホーム > 物理の講義 > 高校で教えない数学
« ロピタルの定理の証明 |
オイラーの公式の使い方
オイラーの公式の使い方
大学に入ると次のような式を学びます。(e:自然対数)
この式はオイラーの公式と呼ばれています。この式を知っていると計算の見通しが良くなるので高校生でも知っておくと良いと思います。そこで、オイラーの公式を複素数に使いオイラーの公式の使い方について考えてみます。
複素数は、
Z=|Z|(cosθ+i sinθ)
と極座標(距離と角度)の形式で表すことができます。
このとき、Z1とZ2の積を考えると、
Z1×Z2=|Z1|(cos(θ1)+i sin(θ1))|Z2|(cos(θ2)+isin(θ2))
=|Z1||Z2|(cos(θ1+θ2)+i sin(θ1+θ2))
となります。
この式の図形的意味を考えると、
(Z1にZ2を掛ける)=(Z1を|Z2|倍に拡大)+(Z1をθ2回転)
というように解釈できます(これは複素数を図形的に考えるときに重要です)。
さて、ここからオイラーの公式を使うと役に立つ理由 を説明します。
上で積を考えたときに,計算で気になるのは、
(cos(θ1)+i sin(θ1))×(cos(θ2)+isin(θ2)) =cos(θ1+θ2)+i sin(θ1+θ2)
の部分です。 この式は、本来なら加法定理を利用して整理すべきものですよね。
しかし,オイラーの公式を使えば、
(cos(θ1)+i sin(θ1))×(cos(θ2)+i sin(θ2)) =(eiθ1)×(eiθ2)
=ei(θ1+θ2) (ea×eb=ea+bを使った)
=cos(θ1+θ2)+i sin(θ1+θ2) (オイラーの公式を使った)
このように指数関数の性質を使い簡単に計算することができます (加法定理の計算を指数関数の積にすることができた)。
また,オイラーの公式を使えばド・モアブルの式は、(eiθ)n = ei nθ という,指数関数の性質である(ea)b=eabのことを言っているだけだということがわかります。
最後にポイントをまとめます。
<Point> オイラーの公式のメリット
Z=|Z|(cosθ+i sinθ)をオイラーの公式を使いZ=|Z|eiθと表すと、めんどくさい三角関数の計算が指数関数の計算に変わるので計算が楽になる。
(指数関数の計算がめんどくさいから対数を取るのと、感覚的には同じ考え方)
Z=|Z|(cosθ+i sinθ)をオイラーの公式を使いZ=|Z|eiθと表すと、めんどくさい三角関数の計算が指数関数の計算に変わるので計算が楽になる。
(指数関数の計算がめんどくさいから対数を取るのと、感覚的には同じ考え方)
<研究>三角関数を指数関数であらわす
オイラーの公式より、
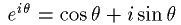 -(1)
-(1)
オイラーの公式の複素共役を取ると、
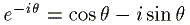 -(2)
-(2)
{(1) + (2)}/2 よりcosが、 {(1) - (2)}/2i よりsinが次のように求まる。
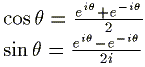
よって、三角関数は指数関数で表された。
オイラーの公式より、
オイラーの公式の複素共役を取ると、
{(1) + (2)}/2 よりcosが、 {(1) - (2)}/2i よりsinが次のように求まる。
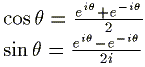
よって、三角関数は指数関数で表された。
ホーム > 物理の講義 > 高校で教えない数学
« ロピタルの定理の証明 |
オイラーの公式の使い方
投稿者 猫背の狸 、更新日 2005年03月15日