物理のための数学
量の変化を表す(微積の準備)
目次
目的
観測によって得られる物理的意味を持った量を物理量と言います。
物理現象を解析するとき、物理量の変化を客観的に知りたいときがあります。
そこで、量の変化を表す方法である、変化量、平均変化率、比例と正比例を今から解説します。
変化量
ある量が変化したとき、量がどれだけ変化したかをあらわすものを変化量と呼びます。
ある量の変化量は、次のように定義します。
(●の変化量)=(●の変化後の量)-(●の変化前の量)
(●の変化量)=Δ●←Δはデルタと呼ぶ
と書くことにすれば、
Δ●=(●の変化後の量)-(●の変化前の量) -(*)←変化量の定義
となります。
この定義は日常生活でもよく使われています。
たとえば、
体重が50Kgから65Kgに太ったとき、
体重の変化量は、(*)より、
Δ(体重)=(体重の変化後の量)-(体重の変化前の量)
=(65Kg)-(50Kg)
=+15Kg
となるので、体重の変化量は+15Kgと求まります。
物理への応用として次の問題を解いてください。
物体がx軸上を動いている。 最初x = +100mの位置にいた物体が、x = -300m移動した。 移動後の位置はどこか?
<解答>
変化量の定義より、
Δ(位置)=(移動後の位置)-(移動前の位置)
⇔(-300m)=(移動後の位置)-(+100m)
⇔(移動後の位置)= -200m
平均変化率
「変化量」で体重の変化の例をあげました。
では、次のような体重の変化に違いはあるのでしょうか。
(1)1年で50Kgから65Kgになった。
(2)半年で50Kgから65Kgになった。
この二つは、どちらも体重の変化量は+15Kgですが、体重が変化した時間(時刻の変化量)が違います。
(1)では時刻の変化量は1年、(2)では時刻の変化量は半年です。
つまり、時刻の変化量に対して体重の変化量が違う、と言うことです。
((2)は半年で15Kg太ったのだから、(1)と同じ1年であれば30Kg太ることになりますよね)
この違いは、時刻の変化量が関係しているので体重の変化量だけでは表現できません。
そこで、2つの量の変化量が関係しているときの変化を表すものとして、平均変化率を定義します。
(▲に対する●の平均変化率)=(●の変化量)/(▲の変化量)
⇔(▲に対する●の平均変化率)=Δ●/Δ▲ -(**)
平均変化率の定義を使えば、
(時刻の変化量に対する体重の平均変化率)=(体重の変化量)/(時刻の変化量)
⇔(時刻の変化量に対する体重の平均変化率)=Δ(体重)/Δ(時刻)
となるので、
((1)の時間に対する体重の平均変化率)
=(+15Kg)/(1年)
=+15kg/年
((2)の時間に対する体重の平均変化率)
=(+15Kg)/(0.5年)
=+30kg/年
この結果から、同じ時間であれば(2)のほうが体重の変化が大きいことが分かる。
物理への応用として次の問題を解いてください。
(1)速度は、時刻の変化に対してどれだけ位置が変化したかを表したものである(速度の定義)。平均変化率の定義を使って速度を表せ。
(2)車が2時間で100Km走った。車の速度を求めよ。
(3)車が速度が60Km/時間(一定)で3時間走った。車の移動距離を求めよ。
<解答>
(1)速度は定義より、
(速度)=(位置の変化量)/(時刻の変化量)=Δ(位置)/Δ(時刻)
(2)速度の定義より、
(速度)
=Δ(位置)/Δ(時刻)
=(100Km)/(2時間)
=+50Km/時間
(注)今求めた速度は、2時間走ったときの平均の速度であって、2時間の常に+50Km/時間であるとは限らない。
(3)速度の定義より、
(速度)=Δ(位置)/Δ(時刻)
⇔(60Km/時間)=Δ(位置)/(3時間)
⇔Δ(位置)=(60Km/時間)×(3時間)=180Km
(注)平均変化率が一定でない、ここでは速度が一定でないとき、今解いたようにすぐに平均変化率の定義を使うことができない。
(2)、(3)の注については、物理のための微積で詳しく解説します。
時刻:時の一点
時間:ある時刻と別の時刻の時の間
つまり、⊿(時刻)= 時間
比例と反比例
2つの量の変化が関係しているときの変化の関係を表すものとして、比例と反比例があります。
・比例
ある量●がa倍になった時、別の量▲もa倍になることを、●は▲に比例すると言い、
●=k▲ (kは定数)
が成立する。
・反比例
ある量●がa倍になった時、別の量■が1/a倍になることを●は■に反比例すると言い、
●=k'/■ (k'は定数)
が成立する。
物理への応用として次の問題を解いてください。
ニュートンの第2法則によれば、質量mの物体に力Fを与えたときに生じる加速度aは力Fに比例し、質量mに反比例する。この関係を式で表せ。
<解答>比例・反比例の定義より、
加速度は力に比例する⇔a=k'F (k'は定数)
加速度は質量に反比例する⇔a=k"/m (k"は定数)
この二つを合わせて、
a=k F/m (kは定数)
↑
●が▲に比例し、■に反比例するとき、
●=k ▲/■ (kは定数)
が成立する。
(参考)
質量1Kgに加速度1m/s2を生じさせる力Fを1Nと定義すれば、
a=k F/m
⇔1 m/s2=k 1N/ 1Kg
⇔1=k ←(m/s2)=(N/Kg)
となり、比例定数kが1になるので、
a=k F/m ⇔ a=F/m ⇔ F=maを得る。
投稿者 猫背の狸 、更新日 2006年12月30日
物理のための微積
目次
目標
微積は物理を定量的(→現象を量で表す)に理解する道具です。
単純な現象のときは、量の変化も単純なので量の変化を表す(微積の準備)で紹介した変化量、平均変化率だけで処理できます。
しかし、複雑な現象になると、微積を使わないと正しく量の変化を表すことができません。
このため、物理を厳密に理解するためには微積が必要不可欠だと言えます。
しかし、微積に慣れていない普通の高校生にとって、微積をどうやって物理に使うのかよくわからないと思います。
そこで、微積にあまり慣れていない人を対象に、物理の世界を理解するのに役立つ直観的な微積の考え方を解説します。
最後のほうで少し微積を使って物理の問題を解くための計算方法についても紹介します。
微積のポイント
微積の考え方の一番重要なポイントをまとめます。
微積の意味がわからない人にはピンと来ないかもしれませんがとりあえず頭に入れてください。
微積とは、微小区間(無限に細かい区間)で考えること。
微小区間では、
・関数の「変数」を「定数」
・図形の「曲線」を「直線」
と近似できる。
ある変数が微小に変化したとき、他の変数の変化はほとんど0に近いので、他の変数の変化は無視して定数とみなそうということです。 当たり前ですが、微小変化まで変化してないとみなしたら何も変化しないことになってしまい意味がなくなります。
□「曲線」を「直線」と近似できるとは
私たちが実感できる例があります。
地球は丸いですね。でも私たちにとって地面は平面に見えます。
これは私たちの見ることができる範囲が、地球の大きさに対してはるかに小さい(微小)からです。
つまり、どんな曲線でもすごく小さい範囲に限定すると直線とみなせるわけです。
これが微積の考え方のエッセンスです。
これから微分の考え方と積分の考え方について詳しく解説していきます。
| 普通の世界 | 微小の世界 | |
| 関数 | 変数 | 定数 |
| 図形 | 曲線 | 直線 |
| 直接計算できない | 直接計算できる |
微分の考え方
微分とは、ある点での変化率、曲線の接線の傾き(直接計算できない)を
平均変化率、直線の傾き(直接計算できる)とみなすことです[表2]。
| 普通の世界 | 微小の世界 | |
| 関数 | ある点での変化率 | 平均変化率 |
| 図形 | 曲線の接線の傾き | 直線の傾き |
| 直接計算できない | 直接計算できる |
微分の考え方が物理に使われていることを、物理量:瞬間の速さを定義することを通して考えていきます。
まず、中学生のときに学んだ速さの定義を確認しましょう。
速さの定義(中学生版):
(時刻t から時刻t+⊿t までの間の速さ)
=(位置の変化量)/(時間の変化量)
文字式で書くと、v = Δr/Δt -(*)
となります。
位置の変化量と時間の変化量がわかれば、この定義式により時刻tから時刻t+⊿tまでの間の速さを求めることができます。
では、瞬間の速さの定義もこの定義(*)を使えばよいのでしょうか?
ちょっと考えてみると、この定義式(*)を瞬間の速さの定義とするには無理があるのに気づきます。
たとえば、10kmを2時間(時刻t から時刻t+2 の間)で走ったとしたら、
速さの定義式(*)により、速さ=5Km/hと求まります。
しかし、2時間走っていて、全ての瞬間で速さが5Km/hとは限らないのではないでしょうか?
ある時刻では休んでいたり、また別の時刻では普段より速く走っているかもしれません。
つまり、(*)の速さの定義式は2時間走ったときの平均の速さを意味していて、走っている間の すべての瞬間の速さを表してはいないのです。
一般的に言い直すと、(*)の速さの定義は時刻t から時刻t+⊿t までの間の時間⊿tの平均の速さであり、時間⊿tの間の全ての時刻での瞬間の速さを表わしてはいない、ということです。
では、このとき瞬間の速さ、たとえば時刻t での瞬間の速さを定義するにはどうすればよいのでしょうか?
上の例で時刻tでの瞬間の速さを求める事ができなかったのは、
速さを測定する時間が⊿t=2時間と長かったため、時刻tでの瞬間の速さから値のずれが大きくなってしまったためと考えられます。
逆に考えれば、速さを測定する時間を小さくすれば瞬間の速さからの値のずれが小さくなり、瞬間の速さに近づくのではないでしょうか。
そこで、瞬間の速さを、平均の速さの定義で測定時間⊿tを限りなく小さくにしたものと定義します。
式で書くと、
瞬間の速さの定義:
瞬間の速さv = limΔt→0 Δr/Δt = dr/dt -(*')
となります。
Δ●→0のときΔ●はd●と表わします。このとき、●に依存する変化量Δ■もd■と表します。
これはある点での変化率は微小区間の平均変化率に一致するという微分の考え方です。
ここまでは瞬間の速さを関数的に考えてきました。
ここからは図形的意味を考えます。
まず準備として、平均の速さΔr/Δtの図形的意味を考えてみましょう。
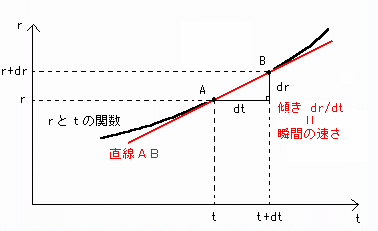
rとtの関数が[図1]のようになっているとき、平均の速さ:Δr/Δtは点A(時刻t)と点B(時刻t+Δt)を通る直線の傾きを表します。
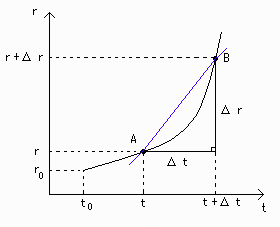
[図1] Δr/Δtの図形的意味
特に、速さが一定のときは、
v=Δr/Δt (=一定)に(t0,r0)と(t,r)を代入して、
v=(r-r0)/(t-t0)
⇒ r=v(t-t0) + r0
となり、rとtの関数は直線になるので、
(rとtの関数の直線の傾き)=(直線ABの傾き)=(速さ)
となります。[図1']
(速さが一定のとき、Δr/Δtは物理的意味を持つ)
これは瞬間の速さを図形的に見るときの伏線になっています。
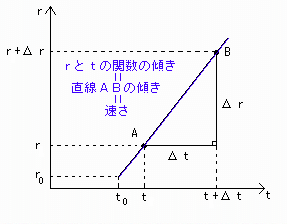
[図1'] 速さvが一定のときのΔr/Δtの図形的意味
ここから瞬間の速さの図形的意味を考えていきます。
瞬間の速さを求めるために測定時間Δtを0に近づけると、
[図2]のように点BはB0→B1→B2→・・・→Bn→・・・と点Aに近づいて行き、最終的に点Aと点Bはほとんど同じ点になります[図2]。
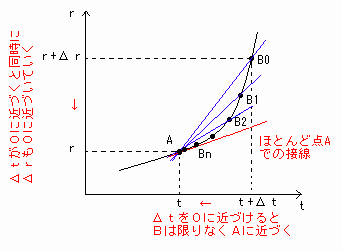
[図2] Δtを0に近づける
このとき、点Aの付近を見てみると、点Aと点Bの間隔が微小になっているため、
rとtの関数の曲線は点AB間で直線に近似でき直線ABと一致しています[図3]。
これは[図1']の状況と同じですよね。
ですから、このときの直線の傾きは瞬間の速さを表しています。
[図3] 点A付近の拡大図
[図3] は点A付近を非常に拡大して見ているので、点Aと点Bは離れているように見えます。
しかし、普通の世界では点Aと点Bはほとんど一致しているので、直線ABは点Aでの接線です。
以上より、瞬間の速さv = limΔt→0 Δr/Δt = dr/dt -(*')の図形的意味は、
r-tグラフの接戦の傾きであると分かりました。
これはある点での接線の傾きは微小区間の直線の傾きに一致するという微分の考え方です。
Δとdの違い
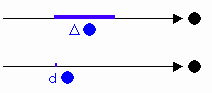
Δ●とd●はどちらも●の変化量を表しています。
Δとdの違いは変化量の大きさにより決まります。
変化量が数値で表せるぐらい大きいときは、Δ●と書き、
変化量が数値で表せないくらい微小なときは、d●と書きます[図4]。
[図4] Δとdの違い
図形的には、Δが測定できる幅を持っているのに対して、
dは幅が測定できないくらい微小で私たちにとって点にしか見えない。
Δとdの違いをふまえれば、
次の2つの運動方程式
m(d2r/(dt)2)=F -(*) と m(Δ2r/(Δt)2)=F -(**)
の違いが見えてきます。
(*)は、私たちには感じられないくらい微小な時間の変化の間(時刻tからt+dt)の運動方程式なので、ある瞬間(時刻t)の運動方程式とみなすことができます。
一方(**)は、時間の変化量がΔtなので、この式は瞬間ではなく一定の時間の間(時刻tからt+Δtの間)での運動方程式を平均したものと考えられます。[図5]
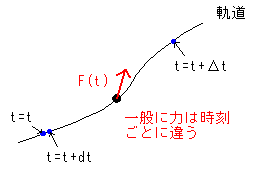
[図5] 運動方程式でのΔとdの違い
d●は必ず微小量の変化を表します。
Δもdも「差」を表していますが、dは日常の概念を超えた「差」を表していることを意識しましょう。
積分の考え方
変数、曲線を無限個の微小な区間に分け、
変数に依存する変化量、曲線で囲まれた図形の面積・体積(直接計算できない)を、
変数に依存しない変化量、直線で囲まれた図形の面積・体積(直接計算できる)の集まり
としてとらえるのが積分です[表3]。
[表3] 積分の考え方
| 普通の世界 | 微小の世界 | |
| 関数 | 変数に依存する 変化量 | 変数に依存しない(定数) の変化量の集まり |
| 図形 | 曲線で囲まれた 面積・体積 | 直線で囲まれた 面積・体積の集まり |
| 直接計算できない | 直接計算できる |
積分の考え方が物理に使われていることを、物理量:移動距離を求めることを通して考えていきます。
まずは、中学で習う方法で考えて見ます。
速さの定義(中学版)・平均の速さ(*)は
Δr = vΔt -(**)
と変形できます。
この式により、速さと時刻の変化量がわかれば移動距離を求めることができます。
たとえば、つねに時速5Km/hで2時間走ったとき、移動距離は(**)より10Kmと求めることができます。
しかし、この式には問題があります。
速さが時刻により変わるとき、どの時刻の速さを代入すればいいのでしょうか?
(**)は平均の速さの式を変形したものなので、ここに代入できるのは一定の速さ(平均の速さは一定)だけなのです。
移動中のどの瞬間の速さでも使えますが、一般的に成立することではありません。
では、一般的に移動距離(時刻tからt+Δtの間移動したとする)を求めるにはどうすればよいのでしょうか?
(**)の式を使って移動距離を求めることができないのは、時間が経過するとともに速さが一定ではなくなるためです。
この問題は、移動時間を無限小な時間に分け、微小な時間ごとに移動距離を求めることによって解決できます。
なぜなら、無限小な時間では速さは瞬間の速さとなり定数とみなせる(ある一瞬の速さだから値は変わらない)からです。
瞬間の速さは定数だから、平均の速さの式(**)から微小時間の間の移動距離を求める事ができます。
それを時刻tからt+⊿t までたし合わせれば全体の移動距離になります。
1秒の間に速度は変わるかもしれませんが、30分の平均速度を使うよりは、正確な移動距離が出そうですよね。1秒よりもっと微小に分ければ、もっと正確な値が出てきます。
式で書くと、
速度が一定でないときも含む移動距離の定義:
微小時間dtの間の移動距離dr= vdt (瞬間の速さの定義より)
時間⊿t の間の移動距離Δr = ∫dr (区間:r(t0)→r(t0+⊿t)) = ∫vdt (区間:t0→t0+⊿t) -(***)
となります。
数列でのΣに対応しています。
Δ●=∫d● (区間:変化前の値→変化後の値)と表されます。
この式は、●の微小変化を集まれば●の変化量となることを意味しています。
これはある区間で変数に依存する変化量を、
区間を微小区間に分けて考えることにより、
変数に依存しない変化量の集まりとみなす
という積分の考え方です。
ここまでは移動距離を関数的に考えてきました。
ここからは図形的意味を考えます。
瞬間の速さのときはr-tグラフを書きましたが、移動距離ではv-tグラフを書きます。
vとtの関数は[図6]にあるように時刻とともに増加していくケースを考えます。
先ほど、Δr = vΔt -(**) は速度一定のときにしか使えないと解説しました。
このことを図形的に確認してみましょう。
(**)に点A(時刻t0)のときの速さv0を代入すると、
Δr = v0Δt となります。
これは[図6]の青色の四角形の斜線部分の面積ですが、速さが変わるときの移動量距離を表していないことは明らかです。
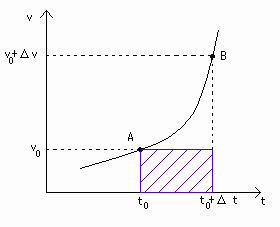 [図6] vΔtの図形的意味
[図6] vΔtの図形的意味
特に、速さが一定のときは、
移動距離Δr = vΔt (v=一定)
⇒ Δr = vΔt(直線)となり、これは[図6']の斜線部分の面積(vとtの直線とt軸を含む四角形の面積)なるので、
(vとtの関数の直線とt軸を含む四角形の面積)=(時間Δtの間の移動距離)-(☆☆)
となります。
(速さが一定のとき、vΔtは物理的意味を持つ)
これは移動距離を図形的に見るときの伏線になっています。
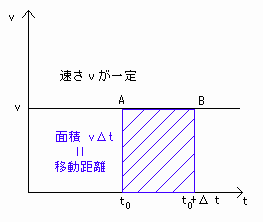
[図6'] 速さが一定のときのvΔtの図形的意味
ここから速度が一定でないときの移動距離の図形的意味を考えていきます。
移動距離を求めるとき、微小時間ごとに移動距離を求めます。
[図7]のように、微小時間dtを取ると、時刻tの付近ではvとtの関数は斜めの直線に近似することができます。
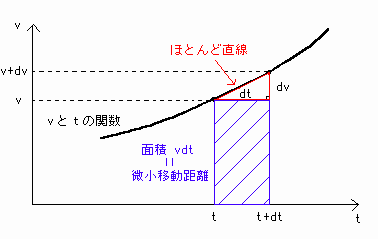
[図7] vdtの図形的意味
このとき、dr = vdt -(**')は、青色の四角形の面積を表します。
実はdr = vdtは青色の四角形の面積であり赤色の三角形を含んだ台形の面積でもあるのです。
日常感覚では理解できませんが、微小な世界では許される話なのです。
実際に、台形の面積を求めると、{v+(v+dv)}dt÷2=vdt+dvdt
でdvdtは微小な数同士の積なので0と近似してよく、結局台形の面積はvdtとなっています。
青色の四角形と赤色の三角形を含む台形の面積が等しいということは、
微小な面積を考えるとき、微小区間dtでvはほとんど一定とみなしてよいということです。
つまり、先ほどvとtの関数は斜めの直線に近似と言いましたが、実際にはほとんど傾きが0の直線に近似されるのです。
これは[図6']の状況と同じなので、vdtの物理的意味は微小時間dtの間の移動距離といえます[図7]。
これより、時間⊿t の間の移動距離Δrの図形的意味が分かります。
定義より、
Δr = ∫dr (区間:r(t0)→r(t0+⊿t))
= ∫vdt (区間:t0→t0+⊿t) -(***)
と表されます。
vdtは微小時間の移動距離であり、v-tグラフにおいて微小な四角形の面積を表しているので、
∫vdt (区間:t0→t0+⊿t)の図形的意味はvとtの関数とt軸で囲まれる部分の面積と分かりました[図8]。
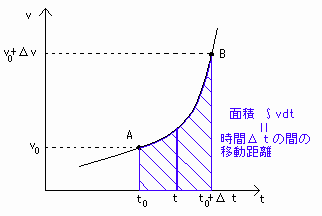
[図8] ∫vdtの図形的意味(区間:t0→t0+⊿t)
このように、微小区間に注目して、
まず微小変化量を求め、
それを足し合わせて全体の変化量を求めることを、
数学の言葉で積分といいます。
微積を使って物理を見る(初心者向け)
今までやってきたことをポイントにまとめます。
今までの話がよくわからなかった人もとりあえずここだけは押さえておきましょう。
- ある▲に対する●の変化率を表す
- ●-▲グラフの接線の傾き
(例)v =dx/dt(■=v(速度)、●=x(位置)、▲=t(時刻))のとき
- あるtに対するxの変化率⇔ある瞬間のxの変化率⇔瞬間の速度
- x-tグラフの接線の傾き
- ●の変化量(区間:●→●+⊿●)
- ■-▲グラフの面積(区間:▲→▲+⊿▲)
(例)∫dx =∫vdt (区間:x0→x0+⊿x、t0→t0+⊿t) (■=v(速度)、●=x(位置)、▲=t(時刻))のとき
- 位置の変化量(区間:x0→x0+⊿x)
- v-tグラフの面積(区間:t0→t0+⊿t)
微分の定義式:■=d●/d▲から求まる微小変化:d●=■d▲を足し合わせることによって求まる。
微積の計算を具体的にしない場合でも、上のポイントは知っておくと、
微積で表わされている式から、グラフの接線の傾きや面積がどんな物理的意味を持っているかが分かります。
たとえば、高校の教科書には電流の定義式:I =ΔQ/Δtとあります。
電荷Qは時刻によって変わる可能性があるので、一般的にはI =dQ/dtと微分を使って表さなくてはいけないことはもうわかりますよね。
上のポイントをふまえれば、微分の意味から、
- ある瞬間の電気量Qの変化率
- Q-tグラフの接線の傾き
また、I =dQ/dt ⇔ 微小変化:dQ =Idtより、
全体の変化:ΔQ = ∫dQ=∫Idt(区間が与えられているとする)が求まります。
この式は積分の意味から、
- ある区間での電気量Qの変化量
- ある区間でのI-tグラフの面積
・力学
速度v =dr/dt
加速度a =dv/dt
仕事W = ∫dW = ∫F・dr
仕事率dW/dt = F・dr/dt
運動量(力積)P = ∫dp = ∫Fdt
・熱力学
気体がする仕事WOUT= ∫dWOUT = ∫PdV
・電磁気
電流I = dQ/dt
電位差V = ∫dV = ∫E・dr
誘導起電力 V = -dΦ/dt
微積を使って問題を解く(上級者向け)
微積を使って力学の問題を解きます。
見慣れていないので複雑に見えると思いますが、高2で習うの微積と合成関数の微分を知っていれば理解できます。
数式を追うだけでなく、物理的意味を考えながら読んでみてください。
(1)物体の運動を求めよ。
(2)物体のエネルギー保存則を導け。
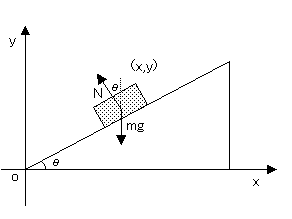
以下では、d●/dt=●'、d2●/dt2=●"と表す。
<解答>
(1)
図のように地面に平行な方向にx軸、垂直な方向にy軸を取る。
・運動方程式
mx"(t)=-Nsinθ (1)
my"(t)=Ncosθ-mg (2)
・初期条件
x(0)=0,y(0)=0 (3)
x'(0)=v0cosθ,y'(0)=v0sinθ (4)
・束縛条件
tanθ=y(t)-y(0)/x(t)-x(0)(物体は常に斜面上にある) [t≠0]
⇒y(t)=tanθx(t) (5) [t=0も含む]
目標:時刻tでの物体の位置(x(t),y(t))を求める。
(1)*cosθ+(2)*sinθよりNを消去:
mx"(t)cosθ+my"(t)sinθ=-mgsinθ
⇔x"(t)cosθ+y"(t)sinθ=-gsinθ (6)
(5)を2回時間微分する:
y"(t)=tanθx"(t) (7) ※d●/dt=●',d●'/dt=●"
(6),(7)よりy"(t)を消去:
x"(t)cosθ+tanθsinθx"(t)=-gsinθ
⇔x"(t)/cosθ = -gsinθ
∴x"(t)=-gsinθcosθ
また、(7)より、y"(t)=-g(sinθ)2
x"(t)=-gsinθcosθと初期条件(3),(4)より、
x'(t)=-gsinθcosθt+v0cosθ
※∫d●=●+C(積分定数) 、初期条件よりC=v0cosθが決まる
x(t)=-(1/2)gsinθcosθt2+v0cosθt
※∫●+C d●=(1/2)●2+C●+D(積分定数) 、初期条件よりD=0が決まる
y"(t)=-g(sinθ)2と初期条件(3),(4)より、
y'(t)=-g(sinθ)2t+v0sinθ
y(t)=-(1/2)g(sinθ)2t2+v0sinθt
(2)
エネルギー保存則を求めます。
運動方程式の両辺に速度をかけると、
(1)*x'(t)+(2)*y'(t) ※仕事率dW/dt=F・V=Fx*Vx+Fy*Vy :
mx"(t)x'(t) + my"(t)y'(t) =-Nsinθx'(t) +Ncosθy'(t) -mgy'(t)
⇔d/dt( (1/2)mx'(t)2+ (1/2)my'(t)2 ) ※d/dt(●2) = 2●●'
= N(-sinθx'(t) +cosθy'(t)) - mgy'(t)
さらに、(5)より-sinθx'(t) +cosθy'(t)=0 ,d/dt(y)=y'より、
⇔d/dt( (1/2)mx'(t)2+ (1/2)my'(t)2 + mgy(t) ) = 0
この式は全ての時刻でエネルギーが一定であることをを表している。
つまり、エネルギー保存則を表す式である。
参考文献
- 図解雑学 微分・積分、図解雑学 わかる微分・積分
0から学ぶ入門書として最適 - 細野真宏の数IIIの微分積分が面白いほどわかる本(微分編)
微分の意味について Section1微分の定義に解説があります。 - 細野真宏の微分積分(原則編)・軌跡が面白いほどわかる本
積分の意味について、1.3.(1)体積の考え方(積分とは?)に解説があります。
投稿者 猫背の狸 、更新日 2007年08月03日
物理のためのベクトル
目次
目標
ベクトルは物理の世界を理解するための道具として大切なものです。
しかし、物理の初心者は、数学としてはベクトルを知っているけれど、物理にベクトルを適用することができないことが多いのです(微積についても同じことが言えます)。これでは物理の体系を効率的に理解することができません。
そこで、この記事では数学にでるベクトルの問題を解くための解説ではなく、どうして、どうやって物理にベクトルを使うのかの解説をします。
ベクトルとは何か?
物理では、物理量(測定により得られる量)を表すために、数学の言葉で言う、スカラーとベクトルを使います。
ここでは、スカラーとベクトルの定義をし、ベクトルの表し方、スカラーとベクトルの違いについて説明します。
● スカラーとベクトルの定義
スカラーとベクトルは次のように定義されています。
- 大きさのみを表すものをスカラー
- 大きさ+向きを表すものをベクトル
● ベクトルの表し方
ベクトルは[図1]のように、
- 矢印の長さ=大きさ
- 矢印の先の向き=向き
として表される。
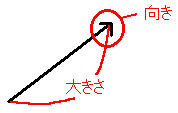
[図1]ベクトルの表し方
● スカラーとベクトルの違い
スカラーとベクトルの違いは、スカラーは向きを示すことができないのに対して、ベクトルは向きを示すことができることです。
この違いを理解していないと、物理量を正確に表すことができなくなります。
なぜベクトルを使うのか?
スカラーとベクトルの違いについては「ベクトルとは何か?」で紹介しました。
では、なぜベクトルを使わなくてはならない場合があるのでしょうか?
次の例題を考えてみてください。
- AとBの距離は5km
- Aから見てBは北東にある
このときスカラーで考えたとき、ベクトルで考えたとき、それぞれAから見てBはどこにあるかを図示しなさい。
<解答>
まず、条件が何を表しているかを考えます。
1は大きさ(距離)についての情報
2は向きについての情報
このことをふまえて、スカラーの場合、ベクトルの場合をそれぞれ考えて行きましょう。
スカラーで考える
スカラーは大きさのみを表すので、1の情報しか使うことができない。
1より、BはAを中心として半径5Kmの円上のどこかにある[図2]。
(2の情報が使えないのでこれ以上Bの位置はわからない)
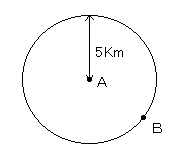
[図2]大きさの情報によるBの図示
このように、スカラーで考えると、Bの位置を完全に確定することができない。
→位置を表すのにスカラーは不適である!
ベクトルで考える
ベクトルは大きさ+向きを表すので、1と2の両方の情報を使うことができる。
まず1より、Aを中心とした半径5Kmの円上にBが位置していると考える事ができる[図2](ここはスカラーと同じ)。
次に2より、BはAからみて北東の向きにあることから[図3]の矢印上のどこかにBが位置していると考えることができる。
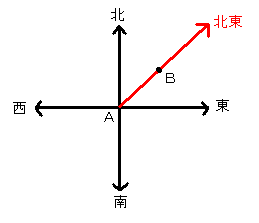
[図3]向きの情報によるBの図示
よって、[図2]と[図3]をあわせて考えれば、
Bは[図2]の円と[図3]の矢印の交点として求まる[図4]。
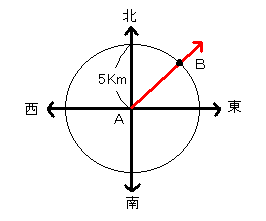
[図4]大きさ+向きの情報によるBの図示
このようにベクトルで考えるとBの位置を正確に定めることができるわけです。つまり、位置を表すのにベクトルは適しているのです。
例題の結果を考えれば、
位置を示すときにはベクトルを使わないと正確に示す事ができないということが分かります。
物理では位置を含めてベクトルを使わないと正確に示すことができない物理量がいくつか存在します(だから物理ではベクトルが必要になる)
(例)位置、速度、加速度、力、・・・
c.f.ベクトルを使わなくても、つまりスカラーで正確に示すことができる物理量もいくつか存在している。
(例)質量、時間、・・・
物理が苦手な人は、ベクトルとスカラーの区別をしていない人が多いので、問題を解くとき物理量はベクトルで表すのか、スカラーで表すのかを意識するようにしましょう。これが物理を得意科目にする第一歩です。
ベクトルの性質
ベクトルの性質について確認します(詳しくは、自分の使っている数学の参考書で確認してください)。
ベクトルは、大きさと向きを使いどの向きにどれだけ移動したかを表します。ベクトルを表示するためには矢印が使われます。
例えば、[図5]の点Aから点Bまでの移動量を![]() と書いてベクトルABと読み、出発する点Aを「始点」、到着する点Bを「終点」といいます。
と書いてベクトルABと読み、出発する点Aを「始点」、到着する点Bを「終点」といいます。
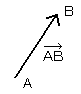
[図5]ベクトルAB
ベクトルは向きと大きさで決まる量なので、2つのベクトル
となるのは、[図6]のように、移動量が同じ、つまり、向きと大きさが同じときに限ります。すなわち、2つの矢印が平行移動で重なるとき、この2つのベクトルは等しいというのです。
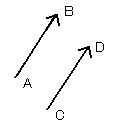
[図6]等しいベクトル
また、2つのベクトル
となるのは、[図7]のように、移動量が反対、つまり、向きが反対で大きさが同じときに限ります。すなわち、2つの矢印が平行移動で反対向きに重なるとき、この2つのベクトルの正負が逆になるのです。
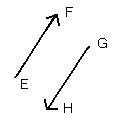
[図7]正負が逆のベクトル
さて、ここからはベクトルの合成、分解について説明します。
次の関係が成り立つのは明らかですよね[図8]。
(点Aから点Bまでの移動量)+(点Bから点Cまでの移動量)
=(点Aから点Cまでの移動量)
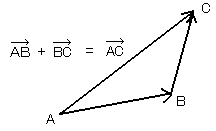
[図8]点Aから点Cへの移動
これをベクトルを使って書けば次のようになります。
![]() +
+![]() =
=![]() -(*)
-(*)
これをベクトルの合成といいます。
一方、(*)を逆から見ると
![]() =
=![]() +
+![]() -(**)
-(**)
これをベクトルの分解といいます。
このように、ベクトルでは、
2つ以上のベクトルを”つないで”1つのベクトルに合成
1つのベクトルを”わけて”2つ以上のベクトルに分解
することができるのです。
物理にベクトルを使うときに役に立つのは、1つのベクトルを”わけて”2つ以上のベクトルに分解できるという性質です。
この性質のおかげで、ベクトルを座標表示することができ、ベクトルを数式として処理する事ができるようになるのです。
ベクトルの座標化
ある点の位置はベクトルを使って[図9]のように図で表すことができます。

[図9]位置ベクトル
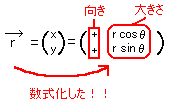
これを式で表すと
だから、図であるベクトルを数式化し計算を行いやすくするために、座標を導入する必要があるのです。
→座標は図形問題を計算問題に変換する働きをする
ベクトルの座標表示の方法をPointにします。
座標は必要に応じて自由に取り入れることができる -(*)
- 原点を決める(注)
- すべてのベクトルが{直線上、平面上、空間上}に存在するとき、
座標軸を{1本、2本、3本}導入する - ベクトルを座標軸上に分解する
- それぞれの軸について、
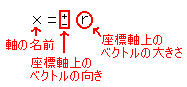 の型で表す
の型で表す
(注)位置ベクトルの始点は原点と一致させる。
上のPointをふまえて、[図9]の位置ベクトル(大きさはr)に座標を導入してみます。
位置ベクトルが直線上にあるとき、[図10]のようにベクトルと同じ向きを正として座標を導入すると、下のようにベクトルを数式化できる。

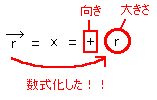
[図10]座標の導入例1
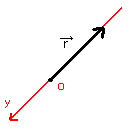
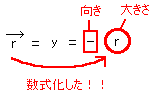
[図11]座標の導入例2
位置ベクトルが平面上にあるとき、[図12]のようにわざとθの角をなすように座標を導入すれば(座標は自由に取り入れる事ができる(普通は計算しやすいように座標を導入する))、下のようにベクトルを数式化できる。
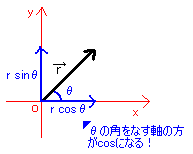
[図12]座標の導入例3
このように、ベクトルを座標表示すれば、ベクトルは数式化され物理の問題に適用しやすくなるのです。
物理が苦手な人は、ベクトルで表される物理量を扱っているときに、スカラーとベクトルの区別ができていない(ベクトルとわかっていない)ので、ベクトルの座標表示をすることができないのです。
そのために、放物運動、鉛直投げ上げ、鉛直投げ下げ、自由落下などの落体の運動を解くときに、お互いを関連づけることができずしかも公式として暗記してしまうのです。位置、速度、加速度がベクトルであることをわかっていれば、ベクトルの座標表示を使えば公式として暗記する必要が無くなることがわかるはずです。
落体の運動を公式として暗記している人は、等加速度直線運動の式
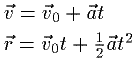
に座標表示した初速度、加速度を代入すれば、公式を暗記しなくても導ける事を確認してみてください。
まとめ
- 物理量はベクトル(大きさ+向き)かスカラー(大きさのみ)で表される
- ベクトルとスカラーの区別をしないと物理量は正確に表すことができない
- ベクトルは座標表示して数式化して計算する
投稿者 猫背の狸 、更新日 2006年12月30日 | コメント (0)
物理のための三角関数
物理で必要になる三角関数関係の公式をまとめました。
ここに出てくる公式、公式の導き方はすぐに使えるようにしましょう。
この程度は押さえていないと、参考書を読むのも大変だと思います。
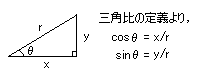
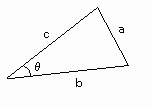
●三角比の定義と定理
[図1]のような角度θ[°]をとる直角三角形において、
sinθ= a/c
cosθ= b/c
tanθ= a/b
と定義する。
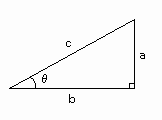
[図1] 三角比の定義
また、定義から次の二つの定理が成り立つ。
tanθ= sinθ/cosθ
(証明)
tanθ=a/b
=(a/c)/(b/c) ←分母分子をcで割った
=sinθ/cosθ←sin,cosの定義を代入した
sin2θ+cos2θ=1
(証明)
sin2θ+cos2θ
=(a/c)2+(b/c)2=(a2+b2)/c2
ここで、三平方の定理より、
a2+b2=c2が成立するので、
sin2θ+cos2θ=1
●余弦定理
[図2]のような三角形において、
a2=b2+c2-2bc cosθ
が成立する。
[図2] 余弦定理
●三角関数の定義と定理
[図3]のように半径1の円で(1,0)から逆時計回りに弧長θ[rad]をとったとき、
その円上の点のy座標をsinθ、x座標をcosθと定義する。
sinθ=y
cosθ=x
また、原点と点(x.y)を通る直線の傾きをtanθと定義する。
tanθ= y/x
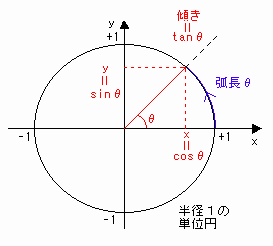
[図3] 三角関数の定義
三角比ではθは度(長さではない単位)を、三角関数ではθは弧長(長さ)を基準とした定義です。 物理ではθが変化する、つまりθを変数とする関数が必要になる場合が出てきます。 しかし、関数は長さを持つものでないと変数として使いにくいので、三角比を三角関数に拡張する必要があります。
<弧度法の定義>
[図4]において、弧長=半径×θ[rad](←弧度法の定義)なので、半径1の単位円では弧長=θ[rad]となります。
θ[rad]は、π[rad]=180[°]の対応関係が成り立つことから、θ[rad]/π[rad]=θ[°]/180[°]が成り立つことを使って求めています。
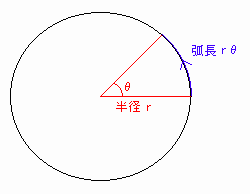
[図4] 弧度法の定義
<円のパラメータ表示>
三角関数の定義を、半径rの円に拡張すれば、
(x、y)=(r cosθ、r sinθ)
となります。
円のパラメータ表示は三角関数の定義を拡張したものなので、x座標sinをy座標cosとすることはできません。
また、定義から次の二つの定理が成り立つ。
tanθ= sinθ/cosθ
(証明)
tanθ=y/x←(0,0)と(x.y)を通る直線の傾き
=sinθ/cosθ←sin,cosの定義を代入した
sin2θ+cos2θ=1
(証明)
sin2θ+cos2θ
=x2+y2
ここで、(x,y)は半径1の単位円上の点なので、
x2+y2=1が成立する。
よって、
sin2θ+cos2θ=1
また、単位円を使えば、
sin(-θ)=-sinθ
cos(-θ)=cosθ
tan(-θ)=-tanθ
sin(π/2-θ)=cosθ
cos(π/2-θ)=sinθ
を得る。
これらの式は、単位円を使って左辺の値は+sinθ、-sinθ、+cosθ、-cosθのいずれに等しいかを考えれば求めることができる。
また、tanについては、tan=sin/cosから求めることができる。
●加法定理
sin(α+β)=sinαcosβ+cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
また、tan(α+β)=sin(α+β)/cos(α+β)より、
tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)
(証明)
tan(α+β)=sin(α+β)/cos(α+β)
=(sinαcosβ+cosαsinβ)/(cosαcosβ-sinαsinβ)
=((sinα/cosα)+(sinβ/cosβ))/(1-(sinαsinβ)/(cosαcosβ))←分母分子をcosαcosβで割った(tanが出てくる形にしたいから)
ここで、tan=sin/cosを使えば、
tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)となる。
また、
・β=-βとすれば、
sin(α-β),cos(α-β),tan(α-β)を得る。
・α=βとすれば、
二倍角の公式、半角の公式を得る。
・A=α+β、B=α-β⇒α=(A+B)/2、β=(A-B)/2とすれば、
和・差の変形公式を得る。
●合成公式
a sinθ + b cosθ =√(a2+b2) sin(θ+φ) (tanφ=b/a)
ただし、φは[図5]を満たすφである。
[図5] 合成公式
投稿者 猫背の狸 、更新日 2006年12月30日