電磁気

電場・電位の概念（初心者用）

目次


目標


電場E・電位Vの意味を一様な重力場と比較して説明します。
初心者向けのかなり荒っぽい解説ですが、電場E、電位Vがさっぱり分からない人には理解のヒントになると思います。

場と場の力

ある空間にいるだけで物体に必ず働く力を場の力といいます。 そのような空間は場とよばれます。 たとえば、私たちのいる地球表面では重力（＝質量m×重力加速度g）がすべての物体に必ず働きます。 だから重力は場の力といえます。そして重力の働く空間である地球は重力場と呼ばれています。

場の力が生まれるのには原因があります。
地球表面の重力場の場合、地球が質量を持っていることによります。

場について興味がある人は、「近接作用」という言葉を調べてみましょう。


電場と電場から受ける力


電気が帯びている周りには電場が発生します。
つまり、電気量q（物体がどれだけ電気を帯びているかを表す物理量）
を持っていることが電場の原因になっているわけです。

ではこのとき電場から受ける力はどのように表されるのかを考えて見ましょう。

まず、地球表面の重力場から受ける力を表す式を考えます。
ご存知のとおり、
重力場から受ける力＝物体の質量m×重力加速度g
と表されます。

これを場という考え方で見て意味づけすると、
・質量mは、重力場が生じた原因の質量に対応している物理量
・重力加速度gは、どんな質量の物体でも共通なものなので、重力場の状態を表している値
と考えることができます。


これらを一般的にまとめると、
場から受ける力
　＝場が生じた原因に対応している物理量×場の状態を表す物理量 (*)
とみなすことができます。

このことをふまえて、電場を重力場の類推でとらえてみましょう。

まず、質量mに対応するものは電気量qです。
重力場の原因は質量であり、電場の原因は電気が帯びていることだからです。
よって、次の対応関係が成り立ちます。
　質量m ⇔ 電気量 q

重力場において場の状態を表す物理量は重力加速度gです。
ここで、電場において場の状態を表す物理量を電場Eと定義します。
そうすると、次の対応関係が成り立ちます。
　重力場の状態g ⇔ 電場 E

以上より、(*)をふまえて、
電場から受ける力F＝電気量q×電場E
と電場から受ける力が表されると類推できます。


電場Eの定義


電場Eの値はどうやって定義し、その物理量を求めることができるのでしょうか。
重力場と対応させて考えていきます。

重力場において、+1Kgの物体に注目すると、F＝mgより、
　F＝+1×g　⇔ F＝g
つまり、
（+1Kgの物体が受ける力の大きさと向き）＝（重力加速度の大きさと向き）
となり、重力場の状態を表す重力加速度を求めることができます。


同様にして、 電場において、+1Cを帯びている物体に注目すると、F＝qEより、
　F=+1×E　⇔ F＝E
つまり、
（+1Cの受ける力の大きさと向き）＝（電場の大きさと向き）
となり、電場を定義し、求めることができるようになります。

地球表面の重力加速度gと違い、電場Eは一般に場所によって違う値をとるので、
定義を使って求めなくてはいけません。


電場の位置エネルギーと電位Vの定義


重力場において、物体は重力場による位置エネルギーをもちます。
同様に、電場においても物体は電場による位置エネルギーをもちます。

地球表面の重力場と対応させて考えると、次のように電場の位置エネルギーを考えることができます。
重力場による位置エネルギーU⇔ mgh＝質量m×g×位置
電場による位置エネルギーU　⇔ 電気量q×E×位置（☆）
（∵質量m ⇔ 電気量 q　、重力場の状態の大きさg ⇔ 電場の大きさE）

一般に、電場の大きさEは位置により変わるので、
電場の大きさEと位置をいっしょに考える（基準量とする）ことにします。

このときの基準量を電位V（つまり、E×位置＝電位V ）とすると、
電場による位置エネルギーU=電気量q×電位V となります。

電位Vの定義は、電場の定義のやり方と同じように+1Cを帯びている物体に注目すると、
　U＝+1×V ⇔ U＝V
となることより、
（+1C の持つ電場によるエネルギー）＝（電位Vの大きさ）と表されます。


まとめ


  • ある空間にいるだけで物体に必ず働く力を場の力という
  • 電場の概念は地球表面の重力場による力:F=mgと対応させると分かりやすい
  • 電場による位置エネルギー、電位の概念は地球表面の重力場の位置エネルギー:U=mghと対応させると分かりやすい

投稿者 猫背の狸 、更新日 2006年12月30日

０からはじめる磁気

目次

  1. 目標
  2. 磁気とはなにか？
  3. 何が磁場をつくるか？ ～電場との比較
  4. 磁場から受ける力
  5. 電磁誘導 ～磁場から電場をつくる

目標

まったく磁気を知らない人でもわかるレベルで、磁気について解説します。

目標は、

  • この記事を読んだ後で問題集の解答を自力で理解できるようになること
  • 自分なりに磁気を視覚化・体系化できるようになること
です。

電気の分野については、空がとっても青いからの大学受験・電気物理が参考になります。


磁気とはなにか？


磁石に他の磁石を近づけると、磁石は互いに引き合ったり反発したりします。

このような現象の根源となるものを磁気といいます。

磁気で働く力は、離れて(接触しないで)力が働く、引き合ったり反発したりする、という点で電気で働く力と類似しています。
電気の世界と対応させながら磁気の世界で何が力が生じる原因をつくるか、どんな力を受けるかについて説明していきます。


何が磁場をつくるか？ ～電場との比較


クーロンの法則 ～静電気力と磁気力との比較


電気におけるクーロンの法則とは、
２つの電荷が静止しているとき、静電気力の大きさFは二つの電荷の間の距離rの2乗に逆比例し、それぞれの電気量q1および q2に比例する
（→F=K(q1q2/r2)というものです。

これに対応するものが磁気に存在していて、磁気でのクーロンの法則は、
磁石の間に働く力を磁極(磁荷)間の力に基づくとみなすと、磁極間の磁気力も静電気力の場合と同様に距離の2乗に逆比例し、それぞれの磁極の磁気量m1およびm2に比例する
（→F=K'(m1m2/r2)というものです。

このように磁気と電気は対応関係にあるので電気で使われた理論が磁気でも同じように使うことができます。

電気の世界では、力Fは電荷qと電場Eを用いて、
F = qE
と表されます。
また、電場の様子は電気力線を使って表されます。

磁気と電気は対応関係にあることをふまえれば、
磁気の世界では、力Fは磁荷mと磁場Hを用いて、
F = mH
と表されると推測できます。
このとき、磁場の様子は磁力線で表されます。

電気と磁気の対応関係
電荷q ⇔ 磁荷m
電場E ⇔ 磁場H
電気力線 ⇔ 磁力線

このような類推は確かに正しいのですがひとつ疑問点があります。
磁荷とはなんなのでしょうか？

電荷はこの世に存在するどんな物質にも含まれています。ガラス棒を絹布で摩擦すると物質は電荷を持つようになる、ということを習ったことがあると思います。

一方、磁荷を取り出す方法を習ったことがあるという人はいないでしょう。
実は、磁荷というものは存在しないからです。

磁石にはN極とS極が存在しています。これは、電荷で言えばプラスとマイナスの電荷に対応するものです。

もし、磁荷が存在しているなら、磁石を細かく切り刻むことにより、単独でN極とS極が表れるはずです。
しかし、磁石をどれだけ細かく切っても、切った端にN極とS極が表れ、単独でN極とS極を得ることはできません。
つまり、磁荷を見つけることができないのです。

では、磁荷が存在しないのなら、何が磁場をつくっているのでしょうか？

＜参考＞磁極
磁極はそういうものがあったほうが都合がよいという事情からできた概念であって現実には存在しません。そのため磁気力のクーロンの法則は、現象論的な法則とみなされています。
しかし、電磁気学の体系自身は磁極が単独で存在できる形になっているし、宇宙に単独の磁極が存在する可能性もないわけではありません。その意味では磁気力のクーロンの法則は、電気力の場合と同じ資格の基礎法則といえます。


何が磁場をつくるのか？


まず、次の問題を考えてください。
<問題>
磁石を細かく切っていけば、つぎつぎと磁石を作ることができる。では、磁石を細かく切る回数に限界はあるか？

答えは、「切る回数に限界はある」です。
磁石を原子(陽子や電子)にまで細かく刻んでしまうと、これ以上は切ることができません。
一番小さい磁石は、原子なのです。

原子では、プラスの電気を持った陽子のまわりでマイナスの電気を持った電子が回転しています。
実は、この電子の回転が磁場をつくる正体なのです。
磁場は、磁荷がつくるのではなく、動いている電荷がつくるのです。


磁場のつくり方


繰り返しますが、動いている電荷が磁場をつくります。

つまり、
電荷が動く　→　磁場が生じる
という因果関係が成立しています。

では、電荷が動くと磁場はどのようにつくられるのでしょうか？

磁場が生じる原因となる電荷の動かし方によって、磁場の生じ方は変わるので、電荷の動かし方で分類します。
（２つの現象に因果の関係があるとき、原因の部分を変えれば結果が変わるだろう、と考えるのは自然な考え方ですよね）

受験では、下の３つの電荷の動かし方しか出ないので覚えてください。

注意　以下では、電荷の集団が動くとき、つまり、電流を流したときに生じる磁場について考える。

＜Case 1＞　電荷を直線に動かす（直線電流）
電荷を直線に動かす（直線導線に電流 I [A]を流す）と、直線導線から半径r [m]離れたところに[図１]のように磁場 H(大きさ= I / 2πr)が生じる。
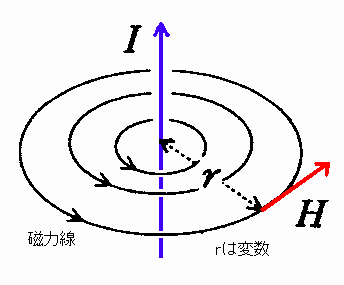
電荷を直線に動かす（直線電流）
[図１] 電荷を直線に動かす（直線電流）


＜Case 2＞　電荷を円形に動かす（円形電流）
電荷を円形に動かす（円形導線に電流 I [A]を流す）と、半径r [m]の円形導線の中心で[図２]のように磁場H(大きさ= I / 2r)が生じる。

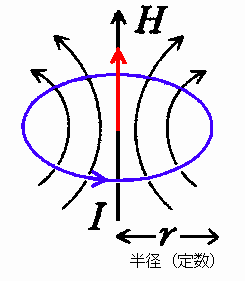
電荷を円形に動かす（円形電流）
[図２] 電荷を円形に動かす（円形電流）


＜Case ３＞　電荷をソレノイドに沿ってに動かす
電荷をコイルに沿って動かす（ソレノイドに電流I [A]を流す）と、ソレノイドの中心で[図３]のように磁場H(大きさ= n I )が生じる。

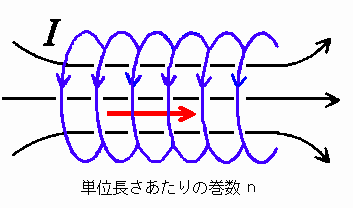
電荷をソレノイドに沿ってに動かす
[図３] 電荷をソレノイドに沿ってに動かす


磁場の向きは、[図４]のように、右ねじを回す向きを磁場Hの向き、右ねじを回すと進む向きを電流Iの向き、と考えればどんな電荷の動かし方の場合でも求めることができます。

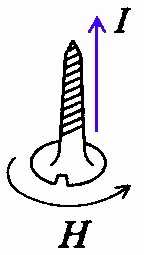
右ねじの法則
[図４] 右ねじの法則


磁束密度Bと磁場Hの関係


磁場の作用で物体が磁石になる現象を磁化といいます。
磁化に注目すると、磁束密度Bと磁場Hには下のような違いがあることがわかります。
  • 磁束密度Bは磁化のしやすさを含む値
  • 磁場Hは磁化のしやすさを含まない値

このとき、磁化のしやすさを表すものとして、透磁率μを使うと、
B=μH
という式が成立します。

磁場での現象は磁化のしやすさも関係するため、磁場Hではなく磁束密度Bで考える必要があります。
さらに詳しい話は、大学レベルの話になるのでここではふれません。

磁束密度Bの別の意味については、電磁誘導のところで説明します。


磁場から受ける力


電場では、電場に電荷を置くと電場から力を受けます。
磁場に電荷を置いても磁場から力を受けません。

では、どうすれば磁場から力を受けるのでしょうか？

その答えは次の実験結果からわかります。

＜実験＞

磁石で作った磁場の中に電線を置き、電流を流さないときと電流を流したときの電線の様子を観察する。

＜結果＞
電流を流さないとき、電線に変化はなかった。
一方、電流を流したとき、電線が曲がった。[図５]

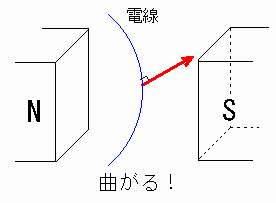
磁場で電荷を動かす
[図５] 磁場で電荷を動かす


この実験の結果から、磁場に電荷を置いただけでは磁場から力を受けないが、電荷を動かす（電流を流す）と磁場から力を受けるということがわかりました。

電荷の数で分類して、磁場から受ける力を２種類に分けます。

＜Case 1　電気を帯びた粒子（荷電粒子）が動く＞
電荷 q [C]の荷電粒子を速度 v [m/s] で動かすと、[図６]のように速度vから磁場 Bの向きに右ねじを回したとき進む方向に大きさF=qvB の力を磁場から受ける。この力をローレンツ力という。 （ただし、速度 vと磁束密度 Bは直交）
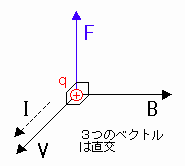
荷電粒子が受ける力
[図６] 荷電粒子が受ける力
（注１）電荷 q が負のとき、力Fの向きは逆になる。 （注２）速度 vと磁場 Bが直交でないとき、速度 vか磁束密度 Bの垂直になる成分を取る。[図７－１]、[図７－２] このとき、どちらで計算しても当然同じF=qvB sinθとなります。
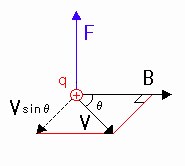
速度の垂直成分をとる
[図７－１] 速度の垂直成分をとる
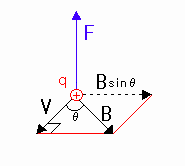
磁束密度の垂直成分をとる
[図７－２] 磁束密度の垂直成分をとる


＜Case ２　電流が流れる（荷電粒子の集団が動く）＞
導線の長さが l[m]の導線に電流 I を流すと、[図６]のように電流I から磁束密度 Bの向きに右ねじを回した方向に大きさ F=IBlの力を磁場から受ける。この力を電磁力という。（ただし、電流 Iと磁束密度 Bは直交）

（注１）電流 I と磁束密度 Bが直交でないときは、電流 I の垂直成分は取れないので、[図７－２]のように磁束密度の垂直成分をとる。このとき、F=I(B sinθ)l
（注２）電磁力は導線内に存在する電子が受ける力の和なので、
（電磁力）＝（導線内に存在する電子の総数）×（ローレンツ力）
が成立している。（この証明はできるようにする）


電磁誘導 ～磁場から電場をつくる

今から、電磁誘導という現象について考えていきます。まずは、準備として磁束密度、磁束線、磁束について説明します。

磁束密度と磁束線の関係


磁束密度と磁束線を関係づけるために、次のように定義します。

定義：磁束密度と磁束線の関係
磁束密度 B のとき、1 m2あたりにB本の磁束線が面を垂直に貫くとする。[図８]

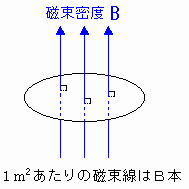
磁束密度と磁束線の関係
[図８]　磁束密度と磁束線の関係


磁束Φ(磁束線の総数)


ある領域Ｓ（面積Ｓm2）に存在する磁束線の総数を磁束Φ、とよぶ。
このとき、定義（磁束密度と磁束線の関係）より、
磁束Φ（磁束線の総数）＝Ｂ×Ｓ
（ただし、磁束線と磁束線を貫く面は垂直（注））[図９]
磁束
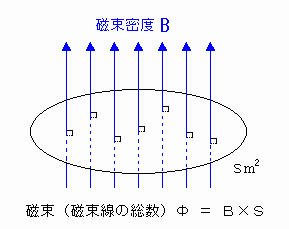
[図９]　磁束


（注）磁束線と磁束線を貫く面が垂直でないとき、定義のように磁束線と面が垂直になるように面の垂直成分[図１０－１]または磁束密度の垂直成分[図１０－２]を取る。

面の垂直成分を取る

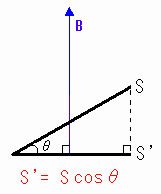
面の垂直成分をとる
[図１０－１]　面の垂直成分をとる

このとき、磁束Φ＝Ｂ×Ｓ’＝Ｂ×Ｓcosθ


磁束密度の垂直成分をとる


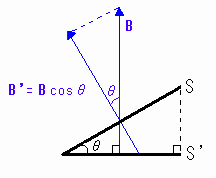
磁束密度の垂直成分をとる
[図１０－２]　磁束密度の垂直成分をとる

このとき、磁束Φ＝Ｂ’×Ｓ＝Ｂcosθ×Ｓ

当たり前ですが、どちらの垂直成分をとっても磁束Φの値は変わりません。


● 電磁誘導とはなにか？


「何が磁場をつくるのか？」で説明したように、
電荷を動かす　→　磁場が生じる　-(*)
という現象が起きるのならば、

逆の現象、つまり、
磁場を生じさせる　→　電荷が動く -(**)
が起きるのではと考えられます。

実験により、確かに(**)が起きることが確認されました。
この現象を電磁誘導と呼びます。


さて、磁場を生じさせるとはどういうことでしょうか？

調べてみると、
磁場を生じさせる＝磁束Φを時間に対して変化させる　-(***)
ということがわかりました。

(**)と(***)をまとめて、電磁誘導とは、
磁束Φを時間に対して変化させる　→　電荷が動く
ということと言えます。

電荷が動くということは、本質的には電場が生じているということ。つまり、電磁誘導とは磁束Φが時間的に変化させると電場が生じる現象、といったほうが正確です。


電磁誘導の意味


電磁誘導とは、磁束を時間に対して変化させると電荷が動くという現象です。
では、電荷が動くと何が起こるのでしょうか。

そこで、磁束密度 Bの場所で導体棒を動かす場合を考えてみましょう。

[図１１]のように導体棒を磁束密度 Bに対して垂直な方向に速度 vで動かす（Φ＝ＢＳのＳの部分を時間に対して変化させる）と、[図１２]のように電荷が動き陽子と電子がそれぞれ導体棒の端に移動する（陽子、電子の動く向きはローレンツ力で説明できる）。

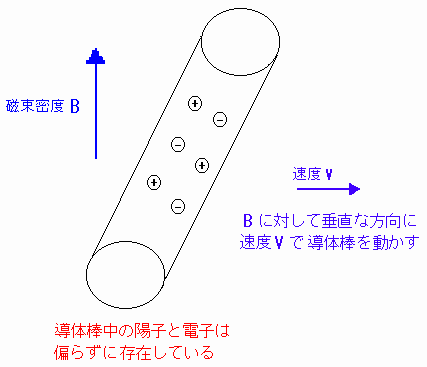
導体棒を磁場で動かす
[図１1]　導体棒を磁場で動かす
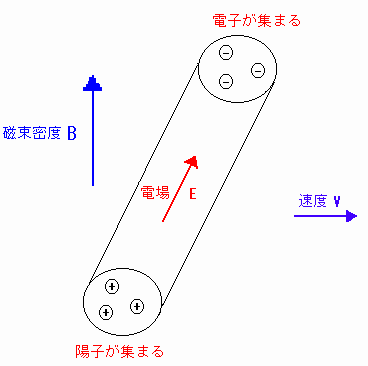
磁場で導体棒を動かした後の状態
[図１２]　磁場で導体棒を動かした後の状態


このとき、電荷が動くことにより、導体棒内で電場 Eが生じ、電位差が生じる。

電位差が生じているので、[図１３]のように導体棒は電池化したと考えることができる。


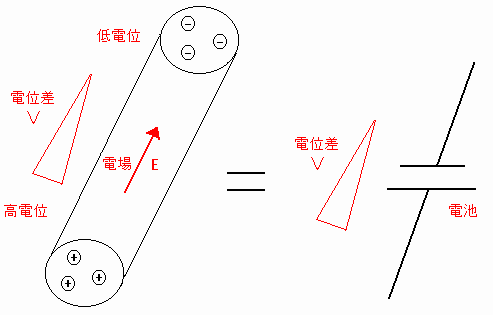
導体棒の電池化
[図１３]　導体棒の電池化

よって、電磁誘導とは導線（コイル）が電池化すること、といえる。
このとき生じる電位差Ｖを誘導起電力と言います。

ちなみに、導体棒に生じる誘導起電力は、後で説明するファラデーの法則を使わなくても、今までの知識で次のように求めることができます。

＜ローレンツ力による電磁誘導の解釈＞

電子の電荷をe、導体棒の長さをlとする。
電子が受ける力は、磁場からの力と電磁誘導が起きたことにより生じた電場からの力を受けます。そして、電子は端で止まっているので、磁場からの力（ローレンツ力）と電場による力はつりあっていることがわかります。
よって、
（電場から受ける力の大きさ）＝（磁場から受ける力の大きさ）
→ｅ Ｅ ＝ｅ v Ｂ
→Ｅ ＝ ｖ Ｂ　-(*)

また、導体棒内では一様な電場が生じているので、
（電位差）＝（電場の大きさ）×（導体棒の長さ）
→Ｖ ＝ Ｅ ｌ　
が成立。
(*)を代入して、
誘導起電力 Ｖ ＝ ｖ Ｂ ｌ
このとき、速度 vから磁束密度 Bの向きに右ねじを回したときにねじの進む向きが高電位となっています。


誘導起電力の求め方（ファラデーの法則）


一般にコイルの誘導起電力を求めるために、ファラデーの法則とレンツの法則を使います。

ファラデーの法則は、
誘導起電力 ｜Ｖ｜ ＝ ｜ΔΦ／Δｔ｜
であり、これから誘導起電力の大きさが求まります。

レンツの法則は、
磁束Φの変化を妨げる方向に誘導起電力は生じる（自然は変化を嫌う）、
というもので、これから誘導起電力の向きが求まります。


このふたつの法則を合わして、
誘導起電力 Ｖ ＝ － ΔΦ／Δｔ　（マイナスの符号がレンツの法則を表している（注））
と表して、これを普通はファラデーの法則とよびます。

ただし、微積を使わないで誘導起電力を求めるときは、誘導起電力の大きさと向きは別々に求めるので、誘導起電力の大きさを決めるのがファラデーの法則、向きを決めるのがレンツの法則と理解したほうが初心者の人にはよいと思います。

（注）マイナスの符号がレンツの法則を表す理由
コイルと同じ形の円形電流[図２]を見てください。
電流の流れる向きを右ネジをまわす向きとすると、右ネジの進む向きに磁場が生じています。このとき、右ネジが進む向きに回す方向の起電力を正とします。

レンツの法則によれば、磁束Φが増加するとき、右ネジが戻る向きに回す方向が高電位となる誘導起電力が生じます。これは、先ほど定義した起電力の向きとは逆なので、マイナスがつきます。
どうやって誘導起電力の向きが決まるかは、次の誘導起電力の向きが決まる仕組みを見てください


（補足）

微積を使えば、誘導起電力 Ｖは、
Ｖ＝－ｄΦ／ｄｔ
と表される。

微積を使えば誘導起電力の大きさと向きを別々に考える必要がなくなり機械的に解けるので、数学が得意な人は使ってみるのもいいかもしれません。
ただし、回路方程式の立て方（ループの向き、電流の向きの設定方法、回路方程式での電池・回路素子の符合の決め方）を分かっていないといけません。


最後に、誘導起電力の向きの決め方を確認します。

＜誘導起電力の向きの決まる仕組み＞
誘導起電力が起きる仕組みは次のようになっています。

レンツの法則より、
磁束Φが増加（減少）したとき、
磁束Φの増加（減少）を妨げるために(I)の向きに磁場Ｂ’が生じる。
（磁束Φ＝ＢＳなので、磁束の変化と逆向きに磁場Ｂ’をつくれば、磁束の変化と逆向きに別の磁束が生じ、磁束の変化を妨げることができる）
このとき、磁場Ｂ’を作るためには、(II)の向きに電流を流せばよく、(II)の向きに電流が流れているとき、コイルに(III)のような電池があると仮想できるので、誘導起電力は(III)のようになる。［図１４］


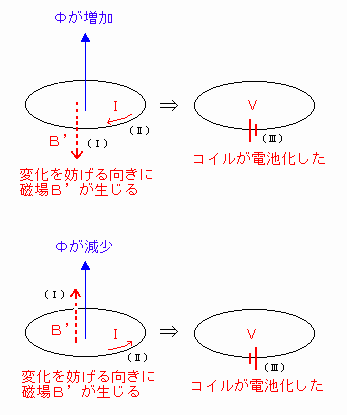
誘導起電力の向き
［図１４］　誘導起電力の向き

投稿者 猫背の狸 、更新日 2006年12月30日

微積を使う交流回路

目次

  1. 目標
  2. 交流回路とはなにか？
  3. 交流回路の電圧
  4. 抵抗，コイル，コンデンサーの電圧
  5. 抵抗，コイル，コンデンサーの電圧を微積を使って求める
  6. 交流回路の位相差
  7. 実効値とはなにか？
  8. 電流の流れにくさを表す
  9. 交流回路の具体例
  10. 最後にアドバイス

目標

微積を物理にあまり使わない人でもわかるレベルで，微積を使う交流回路について講義します．

目標は，微積を使えば交流回路で暗記する必要はないことを知ってもらい，実際に微積を使い問題を解くことができるようになってもらうことです．

交流回路とは何か？

電圧 ｖ，電流 ｉ　が時間 ｔ により sin または cos 的に変化している回路，を交流回路という．

（例）　ｖ＝Ｖ ｓｉｎ（ωｔ + α）　，ｉ＝Ｉ ｃｏｓ（ωｔ + β）

＜Point＞sin，cos　の位相θ（角度）の部分を，θ＝ωｔ + α（β）のように表す方法時刻ｔ＝０の時の位相をα（β）（α，βは定数），時刻ｔ＝ｔの時の位相をθとして，その値を，
角速度の定義 ： ω＝Δθ／Δｔ
に代入すると，
ω＝θ－α（β） ／ｔ－０　←ΔＡ＝（Ａの終わりの値）－（Ａのはじめの値）
⇒θ＝ωｔ + α（β）

（注意） sin と cos は位相θを変えることにより同じ関数を表すことができるから， 交流回路の電圧，電流の関数が sin，cos のどちらでも本質には関係がない．よって，sin と cos のどちらを使ってもよい．
（例） sin (θ+π/2) = cos (θ)，cos (-θ+π/2) = sin (θ)


交流回路の電圧

● 抵抗，コイル，コンデンサーの電圧

抵抗，コイル，コンデンサーの電圧を表す式を確認します[図1]．

抵抗： V = R I (1)
コイル： V = L (d I / dt ) (2) （注）
コンデンサー： Q = C V ⇒　V = Q / C (3)

あと準備として，電流の定義を確認します．

電流の定義： I = dQ / dt (4)

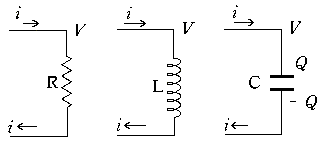
抵抗，コイル，コンデンサーの電圧を表す式
[図1]　抵抗，コイル，コンデンサーの電圧を表す式

（注）(2)のコイルの誘導起電力の式にマイナスがついていない理由

回路を考えるときには，
電池では，低電圧から高電圧の向きを，
回路素子では，高電圧から低電圧の向きを，
電流の流れる向きと定義しています．

コイルに電流を流したとき，誘導起電力は
電流の上流が高電位になり下流が低電位になります．

このとき，
コイルを電池と見れば，
回路での電池の電流の定義の向きと逆なのでマイナスがつきます．

コイルを回路素子と見れば，
回路での回路素子の電流の定義の向きに一致するので，電流の向きの
補正のためのマイナスをつける必要がなくなるのです．

「微積を使う交流回路」では，コイルを電池ではなく回路素子と
みなすことにします．よって，(2)の式にマイナスはつきません．



さらに，数学の準備をします．

三角関数の微分

( sin(f(x)) )' = f'(x) cos(f(x)) (5)
( cos(f(x)) )' = -f'(x) sin(f(x)) (6)

三角関数の積分（三角関数の微分の式の両辺を積分することにより得る）

∫cos(f(x))dx = (1/f'(x))sin(f(x)) (5)'
∫sin(f(x))dx = - (1/f'(x))cos(f(x)) (6)'
（ただし，f(x)は１次式とする）

これだけ押さえておけば微分積分を使い交流を理解することができます．


● 抵抗，コイル，コンデンサーの電圧を微積を使って求める

今から微積を使って考えていきます． 微積を使えば，抵抗，コイル，コンデンサーの電圧をわざわざ覚える必要がなくなります．

電流をi＝Ｉ sin（ωｔ + α）とする．（αが入っているのでこれは交流回路の電流を一般的に表している．詳しい理由はここ．）


まず，抵抗について考えます．
抵抗の電圧の定義式V = R I (1)に，電流i＝Ｉ sin（ωｔ + α）を代入すると，
V = R Ｉ sin（ωｔ + α） (7)
を得る．
これが交流回路での抵抗の電圧です．（これは単に代入しただけですから簡単ですね）

次に，コイルについて考えます．
コイルの電圧の定義式V = L (d I / dt ) (2)に，電流i＝Ｉ sin（ωｔ + α）を代入すると，
V = L (d(Ｉ sin（ωｔ + α）)/dt)
となる．
ここで，d(Ｉ sin（ωｔ + α）)/dtの計算をします．
( sin(f(x)) )' = f'(x) cos(f(x)) (5)より，
d(Ｉ sin（ωｔ + α）)/dt
= I d(sin（ωｔ + α）) （I は定数だから外に出した）
= I (ωｔ + α)' cos（ωｔ + α） （f(x)=ωｔ + α ， f'(x)=(ωｔ + α)'=ω)
=ωI cos（ωｔ + α）

よって，V = ωL I cos（ωｔ + α）
を得る．
これが交流回路でのコイルの電圧です．（電流の微分のところで三角関数が出てるのでちょっと厄介ですね）

最後に，コンデンサーについて考えます．
コンデンサーの電圧の定義式V = Q / C (3)に，抵抗やコイルのように電流i＝Ｉ sin（ωｔ + α）を代入したいのですが 電流の式がコンデンサーの電圧の定義式に含まれていません．
そこで，今から電圧の定義式を電流の式が出てくるように変形します．
電流の定義はI = dQ / dt (4)
この式の両辺にdtを掛ければ，dQ = I dt　となる．
この式の意味は，微小時間dtに流れていく微小電気量dQは 電流 Iと微小時間dtの積に等しいということです．だからこの式で，微小時間dtでの微小電気量dQを全ての時間で足し合わせていけば（積分すれば）， 全体の電気量Qを求めることができます．
式で書けばこういうことです．
∫dQ = ∫I dt
⇒Q = ∫I dt (4)' （この式も電流の定義を表している）
以上で，QをIの式で表すことができました．

このとき，(4)'を(3)に代入すると，
V = ∫I dt / C
となる．
この式に，電流i＝Ｉ sin（ωｔ + α）を代入をすれば，
V = ∫Ｉ sin（ωｔ + α）dt / C
となる．

ここで，∫Ｉ sin（ωｔ + α）dtの計算をします．
∫sin(f(x))dx = - (1/f(x))cos(f(x)) (6)'より，
∫Ｉ sin（ωｔ + α）dt
=Ｉ∫sin（ωｔ + α）dt（I は定数だから外に出した）
= - I (1/(ωｔ + α)') cos（ωｔ + α） （f(x)=ωｔ + α ， f'(x)=(ωｔ + α)'=ω)
= - I (1/ω) cos（ωｔ + α）

よって，V = -(1/ωC) I cos（ωｔ + α）
を得る．
これが交流回路でのコンデンサーの電圧です．（積分の意味を考えて新しく電流の定義を導くところと三角関数の積分が厄介です）

（補足）上の積分の計算で不定積分を行ったとき，積分定数を０とした．なぜなら，もし積分定数が０でなくI0(≠０)だとしたら， 常にコンデンサーに定常電流が存在することになる．しかし，これは明らかに起こり得ない．よって，I0=0（コンデンサーに定常電流は存在しない)とした．


最後に，電圧の求め方をまとめます．
＜Point＞抵抗，コイル，コンデンサーの電圧を微積を使って求める方法
  1. 電流を適当に設定する（たとえば，i＝Ｉ cos（ωｔ + α））
    （もちろん，問題文で電流が指定されているならそれに従う）
  2. 抵抗，コイル，コンデンサーの電圧の定義式（式(1)，(2)，(3)）に１で設定した電流を代入する

＜問題１＞
電流をi＝Ｉ sin（ωｔ + α）として，抵抗，コイル，コンデンサーの電圧を求めよ．

＜解答＞
上の説明を参照．（自分で導けるようにする）


交流回路の位相差

● 位相差の意味について

交流回路では，抵抗，コイル，コンデンサーで位相差があるという話が出てきます．
位相とは三角関数の角度にあたる部分です．位相差とはふたつの式の位相の差をさしています．

たとえば，電流 i = Ｉ sin（ωｔ + α） の位相はωｔ + α， コンデンサーの電圧 V =(1/ωC) Ｉ sin（ωｔ + α + β） の位相はωｔ + α+ βであり，電流に対するのコンデンサーの電圧の位相差は ⊿θ＝（ωｔ + α+ β）-（ωｔ + α）＝ βとなる．

＜位相差を考えるときの注意＞
位相差を考えるとき，ふたつの式の三角関数が同じなら位相以外の部分が違っていてもよい．（上の例で，電流は i = Ｉ sin（ωｔ + α）であり，コンデンサーの電圧はV =(1/ωC) Ｉ sin（ωｔ + α + β）と sinにかかっている値が違っているけれど位相差を考えるときには関係ない）
しかし，三角関数が同じでない（一方が+sinのとき，もう一方が-sin,+cos,-cos）なら位相差を考えることができないので，同じ三角関数にしてから位相差を考える．
（上の例では，電流，コンデンサーの電圧の三角関数が同じ +sinなのですぐに位相差を考えることができた）

位相差の求め方をPointにします．
＜Point＞位相差を求める
  1. 三角関数を同じ型にする
  2. 式A,式Bの位相を求める
  3. Aに対するBの位相差＝（Bの位相）-（Aの位相）に代入する


ここからが本題になりますが，位相差がわかると何がわかるのでしょうか？
まず，位相の意味は，位相とは三角関数の角度の部分だから，位相は三角関数の値を定めると考えることができます．
このとき，位相差の意味は，位相の値が違うのだから，位相差は三角関数の値がどれだけ違う値を取るかを決めると考えることができます．

上のような位相差の解釈はわかりやすいですが，物理現象を考えるのに適した考え方であるとは限りません．そこで，具体例を通して物理現象に適した位相差の意味について考えていきます．

y1= A sin （ωｔ ），y2= B sin （ωｔ + π/2）
のふたつの式において，
（y1の位相）=ωｔ ，（y2の位相）=ωｔ + π/2
であり，y1に対するy2の位相差は，
位相差⊿θ=（ωｔ + π/2）-（ωｔ）=π/2

この位相差は上で考えた位相差の意味をふまえれば，y2はy1に対して位相差π/2分だけ値が常に異なることを意味しています．
図にするとこちらのようになります．（図は新しいウインドウで開きます）
確かに位相差の意味どおりに，どんな時刻でも常にy2はy1に対して位相差π/2分だけ値が常に異なっています．
しかし，このような位相差の考え方を物理現象に適用してもあまり意味がない（現象が見えてこない)ので，位相差があることによって何が起きているかを別の見方で考えていきます．
図を見ると，y2は位相が常にπ/2大きいので，常にy2が最大値をとってから一定時間（=（π/2）/ω（角速度の定義から求めた））経過した後で，y1が最大値をとることがわかります．

つまり，位相差は最大値をとる時刻の違いを表していると考えることができます．
（最初の位相差の解釈はある時間に注目して考えたもので，二つ目の解釈は変位が最大値をとる時間に注目して考えたものです）
＜Point＞位相差

位相差は最大値をとる時刻の違いを表している．
よって，Aに対してBが常に正の位相差があれば，常にBはAより先の時刻に最大値を取り，Aに対してBが常に負の位相差があれば，常にBはAより後の時刻に最大値を取ることわかる．

この位相差の考え方を定常状態の直流回路と交流回路に適用すると，次のようにそれぞれの回路の違いが見えてきます．

定常状態の直流回路では，電流が最大値を取るとき電圧も最大値を取る．
一方，交流回路において電流と電圧に位相差があるとき，電圧が最大値のときに電圧は最大値を取らない．
このことから，交流回路は定常状態の直流回路と違って複雑な働きをしてるだろうと推測できる．


電流に対する抵抗，コイル，コンデンサーの電圧の位相差を求める準備として次の問題を解いてください．（ただの数学の問題です）
＜問題２＞
y0 = sin（ωｔ + α）, y1 = sin（ωｔ + α）, y2 = - sin（ωｔ + α）,
y3 = cos（ωｔ + α）, y4 = - cos（ωｔ + α） とする．
このとき，y0に対するy1,y2,y3,y4の位相差を求めよ．
また，y0～y4が最大値を取る順番を求めよ．


＜解答＞
Point位相差を求める に従って考えます．

Step1.y1～y4をy0の三角関数の型（+sin）と同じにする
y1はy0と同じ型なのでO.K.
y2は，-sin（θ） = sin（θ+π）を使い，
y2 = sin（ωｔ + α+ π）
y3は，cos（θ） = sin（θ+π/2）を使い，
y3 = sin（ωｔ + α+ π/2）
y4は，-cos（θ） = sin（θ-π/2）を使い，
y4 = sin（ωｔ + α+ π/2）
（三角関数の型を変換する式は，左辺の値が+sinのどの位相の値に対応するか単位円またはグラフで考えれば良い）

Step2.y0～y4の位相を求める
（y0の位相）＝ωｔ + α，
（y1の位相）＝ωｔ + α， （y2の位相）＝ωｔ + α+ π，
（y3の位相）＝ωｔ + α+ π/2， （y4の位相）＝ωｔ + α- π/2

Step3.y0に対するy1～y4の位相を求める
（y0に対するy1の位相差）＝0
（y0に対するy2の位相差）＝π
（y0に対するy3の位相差）＝π/2
（y0に対するy4の位相差）＝-π/2


Point位相差 をふまえれば，最大値を取る順番は
y2→y3→y0→y4となる．


● 抵抗，コイル，コンデンサーの位相差を求める

さて，ここから抵抗，コイル，コンデンサーの位相差を求めて行きます．

抵抗，コイル，コンデンサーの電圧を微積を使って求めるで求めたように，
回路の電流がi＝Ｉ sin（ωｔ + α）のとき，
抵抗の電圧：VR = R Ｉ sin（ωｔ + α）
コイルの電圧：VL = ωL I cos（ωｔ + α）
コンデンサーの電圧： VC = -(1/ωC) I cos（ωｔ + α）
となります．

位相差を考えるために，三角関数の型をそろえると（＜問題２＞の解答参照），
回路の電流がi＝Ｉ sin（ωｔ + α）のとき，
抵抗の電圧：VR = R Ｉ sin（ωｔ + α）
コイルの電圧：VL = ωL I sin（ωｔ + α + π/2）
コンデンサーの電圧： VC = (1/ωC) I sin（ωｔ + α- π/2）

このとき，位相差はそれぞれ
（電流の位相）＝ωｔ + α，（抵抗の電圧の位相）＝ωｔ + α，
（コイルの電圧の位相）＝ωｔ + α + π/2，
（コンデンサーの電圧の位相）＝ωｔ + α- π/2
なので，
（電流に対する抵抗の電圧の位相差）＝ 0
（電流に対するコイルの電圧の位相差）＝ +π/2
（電流に対するコンデンサーの電圧の位相差）＝-π/2
となる．

位相差の意味を考えれば，
交流回路では，電流と抵抗の電圧は同じタイミングで最大値を取り，電流に対してコイルの電圧は位相差+π/2の分だけはやく最大値を取り，電流に対してコンデンサーは位相差-π/2の分だけおそく最大値を取ることが分かる．

ちなみに，コイルの電圧が最大のときには電流は最大に達していないという位相差の意味は，コイルは自己誘導により逆起電力が生じるため最大電圧をかけてもすぐには最大電流にはならないという性質に対応しています．

コンデンサーの電流が電圧より先に最大になるという位相差の意味は，コンデンサーに電流が流れ電荷がたまり，電圧が生じるという性質（電流が流れるほうが，電圧が生じるより時刻が常に先になる）に対応しています．

交流回路の動的なイメージがほしい人は，ここが参考になると思います（JAVAを使って位相差の意味が見えるように説明されています)．

実効値とはなにか？

実効値とは，交流の電圧，電流などのように，時間的に変化するものの大きさを示す値の一つで，平均電力が等しくなる直流に換算した値です．わかりやすく言うと，実効値とは交流回路を直流的に考えるために導入したものなのです．

高校物理では，交流回路に微積を使わないので実効値を使い考えることがメインになります．しかし，実効値を使えば直流的に考えることができるとはいっても，実際には交流回路を扱っているので直流回路とまったく同じようにはいきません．そのため，微積を使わずに交流回路を解こうとすると多くの暗記が必要となります．

ここでは，とりあえず実効値を導入します．

回路の電流がi＝Ｉ sin（ωｔ + α）のとき，
抵抗の電圧：VR = R Ｉ sin（ωｔ + α）
コイルの電圧：VL = ωL I sin（ωｔ + α + π/2）
コンデンサーの電圧： VC = (1/ωC) I sin（ωｔ + α- π/2）

このときsin,cosがくっついているのはわずらわしいのでそれぞれの電流，電圧の最大値を取る．
電流の最大値：iMax＝ Ｉ
抵抗の最大電圧：VR,Max = R Ｉ
コイルの最大電圧：VL,Max = ωL I
コンデンサーの最大電圧： VC,Max = (1/ωC) I

さらに，直流らしく考えるために(電流，電圧の実効値）＝1/√2× (電流，電圧の最大値) を取る．
電流の実効値：ie＝1/√2× iMax＝1/√2× Ｉ
抵抗の電圧の実効値：VR,e = 1/√2× VR,Max= 1/√2× R Ｉ= R ie
コイルの電圧の実効値：VL,e = 1/√2× VL,Max = 1/√2× ωL I = ωL ie
コンデンサーの電圧の実効値： VC,e = 1/√2× VC,Max = 1/√2× (1/ωC) I = (1/ωC) ie
（電流計，電圧計の値は実効値）

＜Point＞実効値
  1. 電流，電圧の最大値を取る
  2. (電流，電圧の実効値）＝1/√2×（電流，電圧の最大値）を行う
(注）実効値は最大値を1/√2倍しただけなので，実効値で成立することは最大値でも成立するし，最大値で成立することは実効値でも成立する．

いやに気軽というか簡単に実効値を導入してしまいましたが，この導入には二つの問題があります．それは上でアンダーラインが引かれている部分です（どこがおかしいかわかりますか？）．そこに交流回路に微積を用いないと暗記が必要になる理由が隠されています．

一つ目のアンダーラインの部分については，後で実際に電圧の計算をするとき（「RLC直列回路」）に考えることにして，ここでは参考として二つ目のアンダーラインの部分の説明をしましょう．

二つ目のアンダーラインの部分で疑問なのは何で最大値の1/√2倍が実効値になるのかということです．これは，一番始めに書いたように実効値は平均電力が等しくなる直流に換算した値なので実際に消費電力を求めて正しいかどうか確認しましょう．

＜参考＞消費電力を求める
（ハイレベルの大学では結果を暗記するだけでなく計算ができることが求められます)

回路の電流がi＝Ｉ sin（ωｔ + α）のとき，
抵抗の電圧：VR = R Ｉ sin（ωｔ + α）
コイルの電圧：VL = ωL I cos（ωｔ + α）
コンデンサーの電圧： VC = -(1/ωC) I cos（ωｔ + α）

(消費電力P)=(電圧V)×(電流i)なので，

抵抗の消費電力：PR= RI2 (sin（ωｔ + α）)2 =1/2 RI2 (1 - cos 2(ωｔ + α）)
このとき，1周期（t=0～t=T(=2π/ω)）での抵抗の消費電力は，PRを１周期分時間積分を行えば，
（1周期分の抵抗の消費電力)= 1/2 RI2 * T　となります。
このとき、平均の抵抗の消費電力は、
（平均の抵抗の消費電力)=（１周期分の消費電力）÷（１周期 T）
= 1/2 RI2 = (1/√2× R Ｉ) × (1/√2× Ｉ)
= (抵抗の電圧の実効値)×(電流の実効値)
となっている．
つまり，最大値の1/√2倍を実効値として導入して問題はない．
（厳密には，電力は電圧や電流の2乗に比例するから，実効値を求めるには，2乗し平均をとったものの平方根を計算すればよい．（これは上の説明で納得できない人用の説明です））

コイルの消費電力：PL= ωLI2 (sin（ωｔ + α）cos（ωｔ + α）) =1/2 ωLI2 (sin 2(ωｔ + α）)
このとき，1周期（t=0～t=T(=2π/ω)）でのコイルの消費電力は，PLを１周期分時間積分を行えば，
（1周期分のコイルの消費電力)= 0となるので、
（平均のコイルの消費電力)= 0
（注意）１周期全体では消費電力はないが瞬間瞬間ではPLのように消費電力は存在している．

コンデンサーの消費電力：PC= -(1/ωC)I2 (sin（ωｔ + α）cos（ωｔ + α）) =- 1/2 (1/ωC)I2 (sin 2(ωｔ + α）)
このとき，1周期（t=0～t=T(=2π/ω)）でのコンデンサーの消費電力は，PCを１周期分時間積分を行えば，
（1周期分のコンデンサーの消費電力)= 0となるので、
（平均のコンデンサーの消費電力)= 0
（注意）１周期全体では消費電力はないが瞬間瞬間ではPCのように消費電力は存在している．

<さらに補足>
コイル，コンデンサーでは消費電力が０になっているけれど，実効値はどうなったんだと思うかもしれません．
実効値は交流回路を直流的にしたものですが，完全に直流とは一致していません．
正確には電流に対する電圧の位相差がφのとき，
(消費電力)=（電圧の実効値)×（電流の実効値)×cosφ
となっていて，
コイル，コンデンサーでは位相差がπ/2なので消費電力は０になっています．


電流の流れにくさを表す

「実効値とはなにか？」で実効値を導入しました．実効値とは，交流を直流的に考えるために導入したものです．

直流回路には，抵抗と呼ばれる電流の流れにくさを表す量が存在しています．実効値が直流的なものならば，抵抗に対応するものが存在するはずです．だから今から，交流回路において抵抗に対応するものを定義しましょう．

直流回路では，(電圧)=(抵抗)×(電流)という形を取っていました．
だから，この類推として交流回路において抵抗に対応するのは，
(電圧の実効値)=(交流回路の抵抗)×(電流の実効値) -(*)
となると考えられます． このことをふまえて，抵抗，コイル，コンデンサーにおける電流の流れにくさを表す量を定義します．

回路の電流がi＝Ｉ sin（ωｔ + α）のとき，
抵抗の電圧：VR = R Ｉ sin（ωｔ + α）
コイルの電圧：VL = ωL I sin（ωｔ + α + π/2）
コンデンサーの電圧： VC = (1/ωC) I sin（ωｔ + α- π/2）

最大値を取って，
最大電流：i＝Ｉ
抵抗の最大電圧：VR = R Ｉ
コイルの最大電圧：VL = ωL I
コンデンサーの最大電圧： VC = (1/ωC) I

両辺を 1/√2 倍して実効値を取る．
電流の実効値：ie＝1/√2×Ｉ
抵抗の実効値：VR,e = R ie
コイルの実効値：VL,e = ωL ie
コンデンサーの実効値： VC,e = (1/ωC) ie

(*)より，交流回路において電流の流れにくさを表す量はそれぞれ次のようになる．
抵抗：R（抵抗と呼ぶ），コイル：ωL(リアクタンスと呼ぶ），コンデンサー： 1/ωC(リアクタンスと呼ぶ）


また，抵抗，コイル，コンデンサー単独ではなくて，回路全体で，
(回路の電圧の実効値)=(交流回路全体の抵抗)×(回路の電流の実効値)
が成立するとき，
交流回路全体の抵抗部分はインピーダンスと呼ばれる．

＜Point＞電流の流れにくさ

交流回路における電流の流れにくさは，下の式の(交流回路の抵抗)の部分で表わされる．
(電圧の実効値)=(交流回路の抵抗)×(電流の実効値)


交流回路の具体例

● RLC直列回路

ここからは，実際に交流回路を実際に解いてもらいます．そして，問題を通して微積を使えばインピーダンスなどをわざわざ暗記する必要はないということと，実効値の図形的意味（「実効値とはなにか？」で保留した問題）について知ってもらいます．

＜問題３＞はインピーダンスを暗記する必要が無いことをわかってもらうための問題です．
＜問題３＞
電流i = I0 sin(ωt)のとき，下のRLC直列回路のＡＢ間の電位差VABを求めよ．
また，Ve = Z Ie をみたすインピーダンスZを求めよ．（Ve，Ieは実効値）
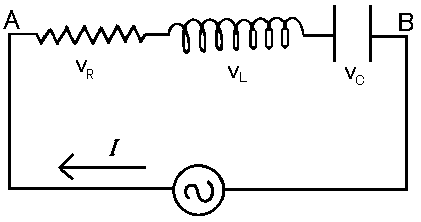
RLC直列回路

＜解答＞
まず，ＡＢ間の電位差VABを求める．
i = I0 sin(ωt)のとき，
VR=Riより，VR=RI0 sin(ωt)
VL=L(di/dt)より，VL=ωLI0 cos(ωt)
VC=∫i dt / Cより，VC=-(1/ωC)I0 cos(ωt)

VAB=VR+VL+VCが成立するので，それぞれの値を代入して，
VAB=RI0 sin(ωt) + (ωL-(1/ωC))I0 cos(ωt)
=√(R2+(ωL-(1/ωC))2) I0sin(ωt+φ)　（電流に対する電圧の位相差はφ,tanφ=(ωL-(1/ωC))/R)
←a sinθ + b cosθ =√(a2+b2) sin(θ+φ) (tanφ=b/a)

次に，Ve = Z Ie をみたすインピーダンスZを求める．
<point>実効値にしたがって考える．
Step1.i,VABの最大値をとる．
iMax= I0
VAB,Max=√(R2+(ωL-(1/ωC))2) I0←sin(ωt+φ)=1のとき最大
Step2.(電流，電圧の実効値）＝1/√2×（電流，電圧の最大値）を行う
Ie=(1/√2)iMax=(1/√2)I0
Ve=(1/√2)VAB,Max=√(R2+(ωL-(1/ωC))2)(1/√2) I0

よって，
Ve=√(R2+(ωL-(1/ωC))2)Ieが成立するので，
インピーダンスZ=√(R2+(ωL-(1/ωC))2)となる．←微積を使えば暗記の必要はない

＜問題４＞は＜問題３＞と中身は同じですが，実効値の図形的意味を知ってもらうための問題です．
＜問題４＞
電流の実効値がIeのとき，下のRLC直列回路においてＡＢ間の電位差の実効値VAB,eを求め，VAB,e = Z Ie をみたすインピーダンスZを求めよ．
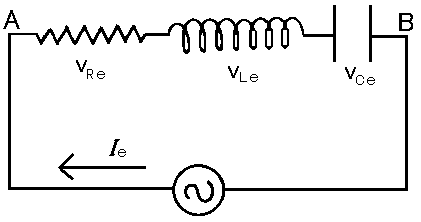
RLC直列回路
＜解答？＞
まずは典型的な誤答から．
抵抗の電圧の実効値：VR,e = R ie
コイルの電圧の実効値：VL,e = ωL ie
コンデンサーの電圧の実効値：VC,e = (1/ωC) ie
が成立する．
このとき，
VAB,e = VR,e + VL,e + VC,eが成立するので，
VAB,e = R ie + ωL ie + (1/ωC) ie = ( R+ωL+(1/ωC))ie
よって，インピーダンスZは，R+ωL+(1/ωC)となる．

上の解答は＜問題３＞の結果とは違っているので間違いですが，どうして間違ってしまったのか分かりますか？
間違えてしまったのは，「実効値とはなにか？」で実効値を導入したときに説明を保留した部分，sin,cosがくっついているのはわずらわしいのでそれぞれの電流，電圧の最大値を取る，を考慮しなかったためなのです．今からこの保留した問題点について解説します．

何が問題なのかと言うと， 実効値⇔最大値なので，実効値の式は電流i，電圧VR，VL，VCが全て最大のときに成立する式です．しかし，電流，電圧間には位相差が存在している（最大値をとる時刻が違う）ので，全ての式が同時に最大値をとることは無いのです．
だから，実効値（⇔最大値）で考えるときには位相を含めて考えなくてはならない（実効値は交流を直流的に考えるために導入したが，実効値を使って電圧を計算するときには直流と同じように単に足し合わせる（スカラー和をとる）方法は使えない）．

位相を含めて考えるために，実効値を使って電圧の計算をするときには，sin,cosのかわりにベクトル表示が使われます．ベクトル表示とは，電流，電圧をベクトルとして考えるもので，大きさは実効値の大きさ，向きは位相によって決まります．

例えば，電流に対して電圧の位相差がφのとき，電圧のベクトルは，電流のベクトルから反時計回りにφ回転した向きに書く[図２]．電圧の計算をするときにはベクトル和を考えることよって，三角関数の代用をすることができるのです．
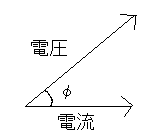
　　　ベクトル表示
[図２]ベクトル表示
ではここから実際にベクトル表示を使い＜問題４＞を解きましょう．
＜解答＞
電流に対して，抵抗の電圧の位相差は０で，コイルの電圧の位相差は +π/2，コンデンサーの電圧の位相差は-π/2なので，ベクトル表示は次のようになる[図３]．
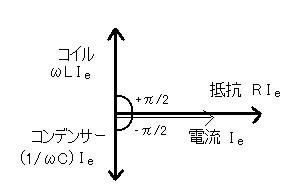
RLC直列回路のベクトル表示
[図3]RLC直列回路のベクトル表示

このとき，３つのベクトルの和を取ると，ＡＢ間の電位差の実効値VAB,eは[図４]の赤矢印の大きさで，電流に対する電圧の位相差はφとなる．
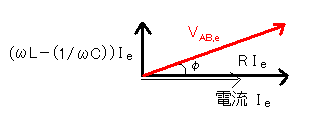
RLC直列回路の電圧の実効値
[図４]RLC直列回路の電圧の実効値


よって，三平方の定理より，VAB,e=√(R2+(ωL-(1/ωC))2)Ie(tanφ=(ωL-(1/ωC))/R)
インピーダンスZ=√(R2+(ωL-(1/ωC))2)となる．←微積を使ったときと同じ結果


最後にアドバイス

以上で，微積を使う交流回路の講義は終わります．微積を使えば交流回路で覚えなくてはいけないことはほとんどないということがわかってもらえたでしょうか？交流回路は出題率が低いですからわざわざ暗記するより，微積を使ったほうがコストパフォーマンスは良いのではないでしょうか．

とりあえず，交流回路で最低限必要になることは全て解説しました（電気振動についてはふれませんでしたが，ばね振り子の類推で考えれば特に問題はないでしょう）．後は，それぞれ自分の使っている問題集で演習をすれば十分です．

より深く交流回路を学びたい人は新・物理入門などの微積を使って物理を解説している参考書・問題集を参考にしてみてください．

投稿者 猫背の狸 、更新日 2006年12月30日