高校で教えない数学
ロピタルの定理の証明
ロピタルの定理
h(x),g(x)が微分可能で,h(a)=g(a)=0のとき,
limx→a h(x)/g(x) = limx→a h'(x)/g'(x) が成立する
⇒h(x),g(x)が微分可能で,h(a)=g(a)=0のとき,
limx→∞ h(x)/g(x) = limx→∞ h'(x)/g'(x) が成立する
⇒h(x),g(x)が微分可能で,h(a)=g(a)=∞のとき,
limx→a h(x)/g(x) = limx→a h'(x)/g'(x) が成立する
h(x),g(x)が微分可能で,h(a)=g(a)=0のとき,
limx→a h(x)/g(x) = limx→a h'(x)/g'(x) が成立する
⇒h(x),g(x)が微分可能で,h(a)=g(a)=0のとき,
limx→∞ h(x)/g(x) = limx→∞ h'(x)/g'(x) が成立する
⇒h(x),g(x)が微分可能で,h(a)=g(a)=∞のとき,
limx→a h(x)/g(x) = limx→a h'(x)/g'(x) が成立する
ロピタルの定理は極限を求めるときに使われる定理です。
この定理を使えば、普通に解くと計算がめんどくさい不定形(0/0や∞/∞)の極限を簡単に求めることができます。
ロピタルの定理を使えばすぐ解けるような入試問題はまず出ないので実用性は低いのですが、一部の受験参考書でも紹介されている定理なので、とりあえず他の受験生に差をつけられないためにも知っておいたほうがよいと思います。
このページでは、問題を通してロピタルの定理の証明と使い方について簡単に説明をします。
ロピタルの定理を使って入試問題を解いてよいのか?
ロピタルの定理は、高校教科書にある定義・定理だけを使って証明することができません。
たとえロピタルの定理が使える問題でも、検算に利用するだけにした方が無難だと思います。 実際、ここのページのように大学レベルの内容を使うことを良く思わない先生もいます。
ロピタルの定理は、高校教科書にある定義・定理だけを使って証明することができません。
たとえロピタルの定理が使える問題でも、検算に利用するだけにした方が無難だと思います。 実際、ここのページのように大学レベルの内容を使うことを良く思わない先生もいます。
<問題>
1.h(x),g(x)が微分可能で,h(a)=g(a)=0のとき,
limx→a h(x)/g(x) = limx→a h'(x)/g'(x) が成立することを示せ.
2.h(x),g(x)が微分可能で,h(a)=g(a)=0のとき,
limx→∞ h(x)/g(x) = limx→∞ h'(x)/g'(x) が成立することを示せ.
3.h(x),g(x)が微分可能で,h(a)=g(a)=∞のとき,
limx→a h(x)/g(x) = limx→a h'(x)/g'(x) が成立することを示せ.
4.limx→∞x1/xを求めよ.
1.h(x),g(x)が微分可能で,h(a)=g(a)=0のとき,
limx→a h(x)/g(x) = limx→a h'(x)/g'(x) が成立することを示せ.
2.h(x),g(x)が微分可能で,h(a)=g(a)=0のとき,
limx→∞ h(x)/g(x) = limx→∞ h'(x)/g'(x) が成立することを示せ.
3.h(x),g(x)が微分可能で,h(a)=g(a)=∞のとき,
limx→a h(x)/g(x) = limx→a h'(x)/g'(x) が成立することを示せ.
4.limx→∞x1/xを求めよ.
<準備>
ロルの定理
a<bとし、関数y=f(x)はf(a)=f(b)をみたすとする。
このとき、a<c<bをみたすあるcが存在して
f'(c)=0 が成り立つ。
ロルの定理は微分学の中心的な定理であり、高校で習う平均値の定理もこの定理から導かれます。
厳密な証明は難しいのでここでは詳しく書きませんが、f(a)=f(b)を満たす連続な関数f(x)のグラフを実際に書いてみれば、直感的にf'(c)=0を満たす点が存在することがわかります。
次に、ロルの定理からコーシーの平均値の定理を導きます。
コーシーの平均値の定理
h(x),g(x)が微分可能のとき、a<x<b内のある点cにおいて
h(b)-h(a) / g(b)-g(a) = h'(c)/g'(c) , a<c<b
が成立する。
ただし、(1)g(a)≠g(b)、(2)f'(x)とg'(x)はa<x<b内で同時に0にならないと仮定する。
[証明]
まず、F(x) = μh(x) - λg(x) として、F(a)=F(b)を満たす、μ,λを定める。
F(a)=F(b)
⇒μh(a) - λg(a) = μh(b) - λg(b)
⇒μ{ h(a) - h(b)} = λ{ g(a) - g(b)}
⇒λ= h(a) - h(b) , μ= g(a) - g(b)
よって、F(x) = { g(a) - g(b)} h(x) - { h(a) - h(b)} g(x) とする。
このとき、ロルの定理より、F'(c)=0が存在するので、
{ g(a) - g(b)} h'(c) - { h(a) - h(b)} g'(c) = 0
⇒{ g(a) - g(b)} h'(c) = { h(a) - h(b)} g'(c) - (*)
ここでg'(c)≠0。
なぜなら、g'(c)=0のとき、(*)より、仮定の(1)をふまえればh'(c)=0となるが、これは仮定の(2)に反する。
よって、(*)の両辺を{ h(a) - h(b)} g'(c)で割れば、
(*)⇒{ g(a) - g(b)} h'(c) / { h(a) - h(b)} g'(c) = 1
⇒h(b)-h(a) / g(b)-g(a) = h'(c)/g'(c)
を得る。(証明終わり)
以上で、ロピタルの定理を証明するための準備は終了です。
<解答>
1.
h(x),g(x)は微分可能で,h(a)=g(a)=0.
コーシーの平均値の定理より、
{h(x)-h(a)} / {g(x)-g(a)} = h'(c)/g'(c)
⇔h(x)/g(x) = h'(c)/g'(c) (☆)
x→a+0 のとき,c→a+0なので,
limx→a+0h(x)/g(x) =limc→a+0 h'(c)/g'(c)
を得る.
同様に,
limx→a-0h(x)/g(x) =limc→a-0 h'(c)/g'(c)
が成り立つ.
よって,
h(x),g(x)が微分可能で,h(a)=g(a)=0のとき,
limx→a h(x)/g(x) = limx→a h'(x)/g'(x)
が成立する.
2.
x=1/tと置き直すと,
limx→∞ h(x)/g(x)=limt→0 h(1/t)/g(1/t)
1.の結果より,
= limt→0 {(-1/t2)h'(1/t)}/ {(-1/t2)g'(1/t)}
= limt→0 h'(1/t)/g'(1/t)
= limx→∞ h'(x)/g'(x)
3.
h(x),g(x)は微分可能で,h(a)=g(a)=∞.
limx→a h(x)/g(x)=limx→a (1/g(x))/(1/h(x))
h(a)=g(a)=∞なので,1/g(a) = 1/h(a) = 0となり,1.の結果より,
limx→a (1/g(x))/(1/h(x))=limx→a (g'(x)/h'(x))×(h2(x)/g2(x))
⇔limx→a h(x)/g(x)=limx→a g'(x)/h'(x)×limx→ah2(x)/g2(x)
⇔limx→a h(x)/g(x)=limx→a g'(x)/h'(x)×(limx→ah(x)/g(x))2
limx→a h(x)/g(x)≠0のとき,
limx→a h(x)/g(x)=limx→a h'(x)/g'(x)
limx→a h(x)/g(x)=0のときは,0にならないように1を加えてから計算する.
つまり,
limx→a h(x)/g(x) +1=limx→a (h(x)+g(x))/g(x)
を考える.
上と同様にして,
limx→a (h(x)+g(x))/g(x)=limx→a (h'(x)+g'(x))/g'(x)
⇔limx→a h(x)/g(x) +1=limx→a h'(x)/g'(x) +1
⇔limx→a h(x)/g(x)=limx→a h'(x)/g'(x)
4.
log (x1/x) = log x/x
limx→∞ log x/x の値を求める.
limx→∞log x=∞,limx→∞x=∞なので,2.と3.の結果より,
limx→∞ log x/x =limx→∞ (1/x)/1=limx→∞ 1/x =0
よって,
limx→∞ log(x1/x)=0⇔limx→∞x1/x=1
投稿者 猫背の狸 、更新日 2006年12月30日
オイラーの公式の使い方
(e:自然対数)
この式はオイラーの公式と呼ばれています。この式を知っていると計算の見通しが良くなるので高校生でも知っておくと良いと思います。そこで、オイラーの公式を複素数に使いオイラーの公式の使い方について考えてみます。
複素数は、
Z=|Z|(cosθ+i sinθ)
と極座標(距離と角度)の形式で表すことができます。
このとき、Z1とZ2の積を考えると、
Z1×Z2=|Z1|(cos(θ1)+i sin(θ1))|Z2|(cos(θ2)+isin(θ2))
=|Z1||Z2|(cos(θ1+θ2)+i sin(θ1+θ2))
となります。
この式の図形的意味を考えると、
(Z1にZ2を掛ける)=(Z1を|Z2|倍に拡大)+(Z1をθ2回転)
というように解釈できます(これは複素数を図形的に考えるときに重要です)。
さて、ここからオイラーの公式を使うと役に立つ理由 を説明します。
上で積を考えたときに,計算で気になるのは、
(cos(θ1)+i sin(θ1))×(cos(θ2)+isin(θ2)) =cos(θ1+θ2)+i sin(θ1+θ2)
の部分です。 この式は、本来なら加法定理を利用して整理すべきものですよね。
しかし,オイラーの公式を使えば、
(cos(θ1)+i sin(θ1))×(cos(θ2)+i sin(θ2)) =(eiθ1)×(eiθ2)
=ei(θ1+θ2) (ea×eb=ea+bを使った)
=cos(θ1+θ2)+i sin(θ1+θ2) (オイラーの公式を使った)
このように指数関数の性質を使い簡単に計算することができます (加法定理の計算を指数関数の積にすることができた)。
また,オイラーの公式を使えばド・モアブルの式は、(eiθ)n = ei nθ という,指数関数の性質である(ea)b=eabのことを言っているだけだということがわかります。
最後にポイントをまとめます。
<Point> オイラーの公式のメリット
Z=|Z|(cosθ+i sinθ)をオイラーの公式を使いZ=|Z|eiθと表すと、めんどくさい三角関数の計算が指数関数の計算に変わるので計算が楽になる。
(指数関数の計算がめんどくさいから対数を取るのと、感覚的には同じ考え方)
Z=|Z|(cosθ+i sinθ)をオイラーの公式を使いZ=|Z|eiθと表すと、めんどくさい三角関数の計算が指数関数の計算に変わるので計算が楽になる。
(指数関数の計算がめんどくさいから対数を取るのと、感覚的には同じ考え方)
<研究>三角関数を指数関数であらわす
オイラーの公式より、
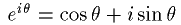 -(1)
-(1)
オイラーの公式の複素共役を取ると、
 -(2)
-(2)
{(1) + (2)}/2 よりcosが、 {(1) - (2)}/2i よりsinが次のように求まる。
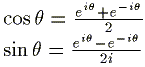
よって、三角関数は指数関数で表された。
オイラーの公式より、
オイラーの公式の複素共役を取ると、
{(1) + (2)}/2 よりcosが、 {(1) - (2)}/2i よりsinが次のように求まる。
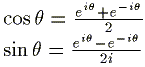
よって、三角関数は指数関数で表された。
投稿者 猫背の狸 、更新日 2005年03月15日